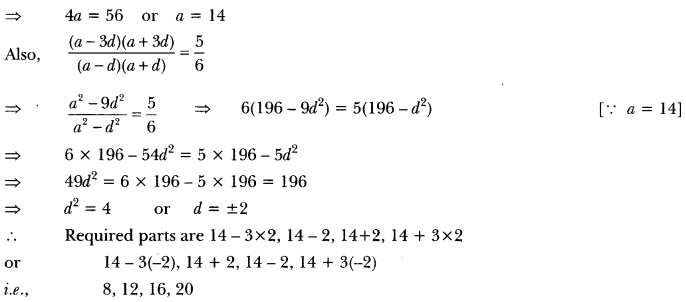We have provided you with Extra and Important Questions from Class 10 Maths Chapter 5 Arithmetic Progressions. This Extra and Important Questions will help you to score 100% in your Board Exams. These extra questions will be helpful to revise the important topics and concepts.

Arithmetic Progressions Class 10 Important Questions with Answers Maths Chapter 5

Extra Questions for Class 10 Maths Chapter 5 Very Short Answer Type

Question: If nth term of an AP is 3+n/4 find its 8th term.

Solution: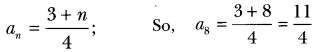

Question:
For what value of p are 2p + 1, 13, 5p – 3, three consecutive terms of AP?

Solution:
since 20 + 1, 13, 5p – 3 are in AP.
∴ second term – First term = Third term – second term
⇒ 13 – (2p + 1) = 5p – 3 – 13
⇒ 13 – 2p – 1 = 5p – 16
⇒ 12 – 2p = 5p – 16
⇒ -7p = – 28
⇒ p = 4

Question:
In a_n AP, if d = -4, n = 7, a, = 4 then find a.

Solution:
We know, a_n = a + (n – 1)d
Putting the values given, we get
⇒ 4 = a + (7 – 1)(-4) or a = 4 + 24
⇒ a = 28

Question:.
Find the 25^th term of the AP: -5, −52 , 0, −52 ……

Solution:
Here, a = -5, b = –52 – (-5) = 52
We know,
a₂₅ = a + (25 – 1 )d
= (-5) + 24(52) = -5 + 60 = 55

Question:
Find the common difference of an AP in which a₁₈ – a₁₄ = 32.

Solution:
Given, a₁₈ – a₁₄ = 32
⇒ (a + 17d) – (a + 13d) = 32
⇒ 17d – 13d = 32 or d = 324

Question: If 7 times the 7th term of an AP is equal to 11 times its 11th term, then find its 18th term.

Solution:
Given, 7a₇= 11a₁₁
⇒ 7(a + 6d) = 11(a + 100) or 7a + 42d = 11a + 110d
⇒ 4a + 68d = 0 or a + 17d = 0
Now, a₁₈ = a + 17d = 0

Question: Which of the following can be the nth term of an AP?
4n + 3, 3n² + 5, n² + 1 give reason.

Solution:
4n + 3 because n^th term of a_n AP ca_n only be a linear relation in n as a_n = a + (n – 1)d.

Question:
Is 144 a term of the AP: 3, 7, 11, …? Justify your answer.

Solution:
No, because here a = 3 a_n odd number and d = 4 which is even. so, sum of odd and even must be odd whereas 144 is a_n even number.

Question: In an AP, if a = 1, a_n = 20, and s_n = 399, then find n.

Solution:
Given, An = 20
= 1 + (n – 1)d = 20
⇒ (n – 1) d = 19
s_n = n2 {2a + (n – 1)d}
⇒ 399 = n2{2 × 1 + 19}
⇒ 399×221 = n
⇒ n = 38

Question:
Find the 9th term from the end (towards the first term) of the AP 5, 9, 13, …, 185.

Solution:
l = 185, d = 4
l₉ = l – (n – 1) d
= 185 – 8 × 4 = 153

Question: If the sum of the first p terms of an AP is ap² + bp, find its common difference.

Solution:
a_p = s_p – s_p-1 = (ap² + bp) -[a(p – 1)² + b(p – 1)]
= ap² + bp – (ap² + a – 2ap + bp – b)
= ap² + bp – ap² – a + 2ap – bp + b = 2ap + b-a .
= a₁ = 2a + b – a = a + b and a₂ = 4a + b – a = 3a + b
⇒ d = a₂ – a₁ = (3a + b) – (a + b) = 2a

Extra Questions for Class 10 Maths Chapter 5 Short Answer Type

Question: In which of the following situations, does the list of numbers involved to make an AP? If yes, give a reason.
(i) The cost of digging a well after every meter of digging, when it costs 150 for the first meter and rises by 50 for each subsequent meter.
(ii) The amount of money in the account every year, when 10,000 is deposited at simple interest at 8% per annum.

Solution:
(i) The numbers involved are 150, 200, 250, 300, …
Here 200 -150 = 250 – 200 = 300 – 250 and so on
∴ It forms a_n AP with a = 150, d = 50

(ii) The numbers involved are 10,800, 11,600, 12,400, …
which forms a_n AP with a = 10,800 and d = 800.

Question:
Find the 20^th term from the last term of the AP: 3, 8, 13, …, 253.

Solution:
We have, last term = 1 = 253
And, common difference d = 2^nd term – 1^st term = 8 – 3 = 5
Therefore, 20^th term from end = 1 -(20 – 1) × d = 253 – 19 × 5 = 253 – 95 = 158.

Question: The first and the last terms of an AP are 5 and 45 respectively. If the sum of all its terms is 400, find its common difference.

Solution:
Let the first term be ‘a’ and common difference be ‘d’.
Given, a = 5, T_n = 45, s_n = 400 .
Tn = a + (m – 1)d
⇒ 45 = 5 + (m – 1)d
⇒ (n – 1) d = 40 ………(i)
s_n = n/2 (a + T_n)
⇒ 400 = n/2 (5 + 45)
⇒ n = 2 × 8 = 16 substituting the value of n in (i)
⇒ (16 – 1)d = 40
⇒ d = 40/15 = 8/3

Question:
Find the number of natural numbers between 101 and 999 which are divisible by both 2 and 5.

Solution:
Natural numbers between 101 and 999 divisible by both 2 and 5 are 110, 120, … 990.
so, a1 = 110, d = 10, a_n = 990
We know, a_n = a₁ + (n – 1)d
990 = 110 + (n – 1) 10
(n – 1) = 990−11010
⇒ n = 88 + 1 = 89

Question: What is the common difference of an AP in which a₂₁ – a₇ = 84?

Solution:
Given: a₂₁ – a₇ = 84
⇒ (a + 20d) – (a + 6d) = 84
⇒ 14d = 84
⇒ d = 6

Question:
For what value of n, are the n^th terms of two APs 63, 65, 67,… and 3, 10, 17,… equal?

Solution:
Let nth terms for two given series be a_n and a’_n
According to questions
a_n = a’_n
⇒ a + (n – 1)d = a + (n – 1)d’
⇒ 63 + (n – 1)2 = 3 + (n – 1)7
⇒ 5n = 65
⇒ n = 13.

Question: In an AP: given l = 28, s = 144, and there are total 9 terms. Find a.

Solution:
We have, l = 28, s = 144 and n = 9
Now, l = a_n = 28
28 = a + (n – 1) d 28 = a + (9 – 1)d
⇒ 28 = a + 8d ……(i)
and S = 144
⇒ 141 = 12 [2a + (n – 1)d]
⇒ 144 = 92 [12a +(9 – 1) d]
144×29 = 2a + 8d
⇒ 32 = 2a + 8d
⇒ 16 = a + 4d … (ii)
Now, subtracting equation (ii) from (i), we get
4d = 12 or d = 3
Putting the value of d in equation (i), we have
a + 8 × 3 = 28
⇒ a + 24 = 28
⇒ a = 28 – 24
∴ a = 4.

Question:
How many terms of the AP: 9, 17, 25, … must be taken to give a sum of 636?

Solution:
Let sum of n terms be 636.
s_n = 636, a = 9, d = 17 – 9 = 8
⇒ n/2[2a + (n – 1) d] = 636
⇒ n/2[2 x 9 + (n – 1) × 8] = 636
⇒ n/2 × 2[9+ (n – 1) 4] = 636
⇒ n[9 + 4n – 4] = 636
⇒ n[5 + 4n] = 636
⇒ 5n + 4n² = 636
⇒ 4n² + 5n – 636 = 0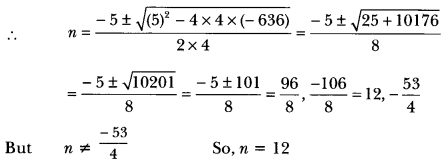

Thus, the sum of 12 terms of given AP is 636.

Question:
The first term, common difference and last term of an AP are 12, 6 and 252 respectively. Find the sum of all terms of this AP.

Solution:
We have, a = 12, d = 6 and l = 252
Now, l = 252
⇒ a_n = 252
= l = a + (n – 1)d
⇒ 252 = 12 + (n – 1) × 6
⇒ 240 = (n – 1) × 6
⇒ n – 1 = 40 or n = 41
Thus, S_n = n2(a + l)
⇒ S₄₁ = 412(12 + 252) = 412 (264) = 41 × 132 = 5412

Question:
If the sum of first 7 terms of an AP is 49 and that of 17 terms is 289, find the sum of first n terms.

Solution:
We have, S₇ = 49
⇒ 49 = 72[2a + (7 – 1) × d]
⇒ 49 × 27 = 2a + 6d
⇒ 14 = 2a + 6d
⇒ a + 3d = 7
and S₁₇ = 289
⇒ 289 = 172 [2a + (17 – 1)d]
⇒ 2a + 16d = 289×217 = 34
⇒ a + 8d = 17
Now, subtracting equation (i) from (ii), we have
5d = 10 ⇒ d = 2
Putting the value of d in equation (i), we have
a + 3 × 2 = 7
⇒ a = 7 – 6 = 1
Here, a = 1 and d = 2
Now, s_n = n2 [2a + (n – 1) d]
= n/2 [2 × 1 + (n – 1) × 2]
= n/2[2 + 2n – 2]
= n/2 × 2n = n²

Question:.
The first term of an AP is 5, the last term is 45 and the sum is 400. Find the number of terms and the common difference.

Solution: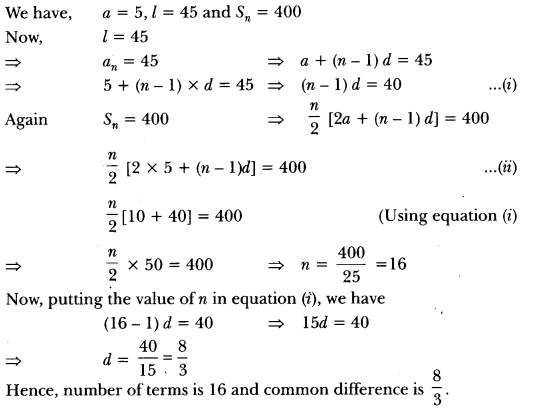

Question:
If the seventh term of an AP is a and its ninth term is, find its 63^rd term.

Solution: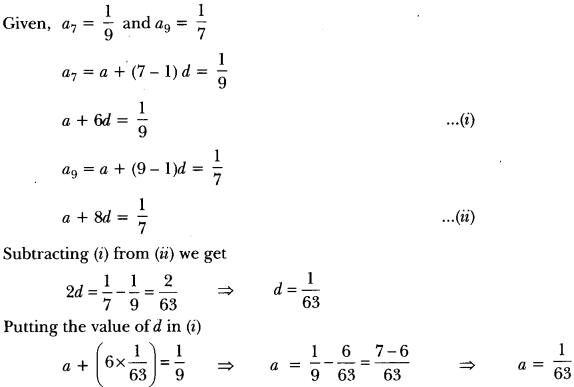

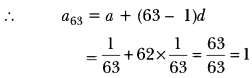
Question: The sum of the first 7 terms of an AP is 63 and the sum of its next 7 terms is 161. Find the 28th term of this AP.
Solution:
sum of first seven terms,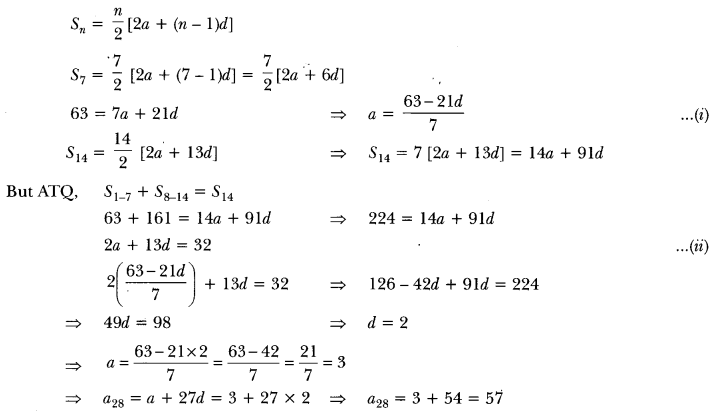

Question:
If the ratio of the sum of first n terms of two AP’s is (7n + 1): (4n + 27), find the ratio of their mth terms.

Solution: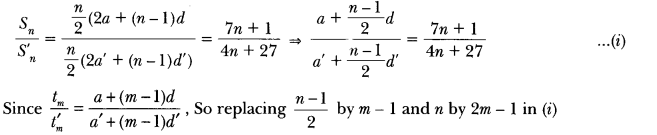

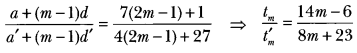
Extra Questions for Class 10 Maths Chapter 5 Long Answer Type

Question: In an AP of 50 terms, the sum of first 10 terms is 210 and the sum of its last 15 terms is 2565. Find the AP.

Solution:
Let ‘a’ be the first term and ‘d be the common difference.


Question:
A thief runs with a uniform speed of 100 m/minute. After one minute a policeman runs after the thief to catch him. He goes with a speed of 100 m/minute in the first minute and increases his speed by 10 m/minute every succeeding minute. After how many minutes the policeman will catch the thief?

Solution:
Let total time be n minutes
Total distance covered by thief = 100 n metres
Total distance covered by policeman = 100 + 110 + 120 + … + (n – 1) terms
∴ 100m = n−12 [100(2) + (n – 2)10]
⇒ 200n = (n – 1)(180 + 10n)
⇒ 10²– 30n – 180 = 0
⇒ n² – 3n – 18 = 0
⇒ (n-6) (n + 3) = 0
⇒ n = 6
Policeman took (n – 1) = (6 – 1) = 5 minutes to catch the thief.

Question: The sum of the 4th and 8th term of an AP is 24 and the sum of the 6th and 10th term is 44. Find the first three terms of the AP.

Solution:
We have, a₄ + a₈ = 24
⇒ a + (4 – 1)d + a + (8 – 1) d = 24
⇒ 2a + 3d + 7d = 24
⇒ 2a + 10d = 24
⇒ 2(a + 5d) = 24
∴ a + 5d = 12
and, a₆ + a₁₀ = 44
⇒ a + (6 – 1)d + a + (10 – 1) d = 44
⇒ 2a + 5d + 9d = 44
⇒ 2a + 14d = 44
⇒ a + 7d = 22
subtracting (i) from (ii), we have
2d = 10
∴d = 102 = 5
Putting the value of d in equation (i), we have
a + 5 × 5 = 12
⇒ a = 12 – 25 = -13
Here, a = -13, d = 5
Hence, first three terms are
-13, -13, + 5, -13 + 2 × 5 i.e., -13, -8, -3

Question:
The sum of the first n terms of an AP is given by s_n = 3n² – 4n. Determine the AP and the 12^th term.

Solution:
We have, s_n = 3n² – 4n …(i)
Replacing n by (n – 1), we get
s_n-1 = 3(n – 1)² – 4(n – 1) ….(ii)
We know, .
a_n = s_n – s_n-1 = {3n² – 4n} – {3(n – 1)² – 4(n – 1)}.
= {3n² – 4n} – {3n² + 3 – 6n – 4n + 4}
= 3n² – 4n – 3n² – 3 + 6n + 4n – 4 = 6n – 7
so, nth term a_n = 6n – 7
To get the AP, substituting n = 1, 2, 3… respectively in (iii), we get
a₁ = 6 × 1-7 = -1,
a₂ = 6 × 2 – 7 = 5
a₃ = 6 × 3 – 7 = 11,…
Hence, AP is – 1,5, 1:1, …
Also, to get 12th term, substituting n = 12 in (iii), we get
a₁₂ = 6 × 12 – 7 = 72 – 7 = 65

Question:
Divide 56 into four parts which are in AP such that the ratio of product of extremes to the product of means is 5 : 6.

Solution:
Let the four parts be a – 3d, a-d, a + d, a + 3d.
Given, (a – 3d) + (a – d) + (a + d) + (a + 3d) = 56