We have provided you with Extra and Important Questions from Class 10 Maths Chapter 4 Quadratic Equations.This Extra and Important Questions will help you to score 100% in your Board Exams. These extra questions will be helpful to revise the important topics and concepts.

Quadratic Equations Class 10 Important Questions with Answers Maths Chapter 4

Extra Questions for Class 10 Maths Chapter 4 Very Short Answer Type

Question: If a and b are the roots of the equation x² + ax – b = 0, then find a and b.

Solution:
Sum of the roots = a + b = – B/A = – a
Product of the roots = ab = B/A = – b
= a + b = – a and ab = -b
⇒ 2a = -b and a = -1
⇒ b = 2 and a = -1

Question:
Show that x = – 2 is a solution of 3x² + 13x + 14 = 0.

Solution:
Put the value of x in the quadratic equation,
⇒ LHS = 3x² + 13x + 14
⇒ 3(-2)² + 13(-2) + 14
⇒ 12 – 26 + 14 = 0
⇒ RHS Hence, x = -2 is a solution.

Question:
Find the discriminant of the quadratic equation 4√2x² + 8x + 2√2 = 0).

Solution:
D = 62 – 4ac = (8)² – 4(4√2)(2√2)
⇒ 64 – 64 = 0

Question: What will be the nature of roots of quadratic equation 2x² + 4x – n = 0?

Solution:
D = b² – 4ac
⇒ 4² – 4 x 2 (-7)
⇒ 16 + 56 = 72 > 0
Hence, roots of quadratic equation are real and unequal.

Question:
If 12 is a root of the equation x² + kx – 54 = 0, then find the value of k.

Solution:
∴ 12 is a root of quadratic equation.
∴ It must satisfy the quadratic equation.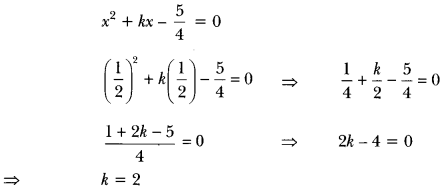

Question: If ax² + bx + c = 0 has equal roots, find the value of c.

Solution:
For equal roots D = 0
i.e., b² – 4ac = 0
⇒ b² = 4 ac
⇒ c = b24a

Question: State whether the equation (x + 1)(x – 2) + x = 0 has two distinct real roots or not. Justify your answer.

Solution:
(x + 1)(x – 2) + x = 0
⇒ x² – x – 2 + x = 0
⇒ x² – 2 = 0
D = b² – 4ac
⇒ (-4(1)(-2) = 8 > 0
∴ Given equation has two distinct real roots.

Question:
Is 0.3 a root of the equation x² – 0.9 = 0? Justify.

Solution:
∵ 0.3 is a root of the equation x² – 0.9 = 0
∴ x² – 0.9 = (0.3)² – 0.9 = 0.09 – 0.9 ≠ 0
Hence, 0.3 is not a root of given equation.

Question:
For what value of k, is 3 a root of the equation 2x² + x + k = 0?

Solution:
3 is a root of 2x² + x + k = 0, when
⇒ 2(3)² + 3 + k = 0
⇒ 18+ 3 + k = 0
⇒ k = – 21

Question:
Find the values of k for which the quadratic equation 9x² – 3kx + k = 0 has equal roots.

Solution:
For equal roots:
D = 0
⇒ b² – 4ac = 0
⇒ (- 3k)² – 4 × 9 × k = 0
⇒ 9k² = 36k
⇒ k = 4

Question:
Find the value of k for which the equation x² + k(2x + k – 1)+ 2 = 0 has real and equal roots.

Solution:
Given quadratic equation: x² + k(2x + k-1) + 2 = 0)
= x² + 2kx + (k² – k + 2) = 0
For equal roots, b² – 4ac = 0
⇒ 4k² – 4k² + 4k – 8 = 0
⇒ 4k = 8
⇒ k = 2

Question:
If -5 is a root of the quadratic equation 2x² + px – 15 = 0 and the quadratic equation p(x² + x) + k = 0 has equal roots, then find the value of k.

Solution:
Since – 5 is a root of the equation 2x² + px – 15 = 0
∴ 2(-5)² + p(-5) – 15 = 0
⇒ 50 – 5p – 15 = 0 or 5p = 35 or p = 7
Again p(x² + x) + k = 0 or 7x² + 7x + k = 0 has equal roots
∴ D = 0
i.e., b² – 4ac = 0 or 49- 4 × 7k = 0
⇒ k = 4928 = 74

Extra Questions for Class 10 Maths Chapter 4 Short Answer Type

Question: Find the value of p, for which one root of the quadratic equation px² – 14x + 8 = 0 is 6 times the other.

Solution:
Let the roots of the given equation be a and 6α.
Thus the quadratic equation is (x – a) (x – 6α) = 0
⇒ x² – 7αx + 6α² = 0 …(i)
Given equation can be written as

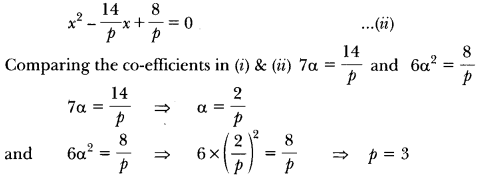
Question: If ad ≠ bc, then prove that the equation
(a² + b²) x² + 2(ac + bd)x + (c²+ d²) = 0 has no real roots.

Solution:
The given quadratic equation is (a² + b²⁾x² + 2(ac + bd)x +(c²+ d²) = 0
D = b² – 4ac
= 4(ac + bd)² – 4(a² + b²) (c²+ d²)
= -4(a²d² + b²c²– 2abcd) = – 4(ad – bc)²
Since ad ≠ bc
Therefore D < 0
Hence, the equation has no real roots.

Question:
Solve for x: √13x² – 2x – 8√3 = 0

Solution:
√3x² – 2x – 8√3 = 0
By mid term splitting
⇒ √3x² – 6x + 4x – 8√3 = 0
⇒ √3x(x – 2/3) + 4 (x – 2/3) = 0
⇒ (x – 2√3)(√3x + 4) = 0
⇒ Either (x – 2√3) = 0 or (√3x + 4) = 0
⇒ x = −43√, 2√3

Question: If x = 2/3 and x = -3 are roots of the quadratic equation ax² + 7x + b = 0, find the values of a and b.

Solution:
Let us assume the quadratic equation be Ax² + Bx + C = 0.
Sum of the roots = –B/A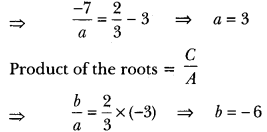

Question:
A two-digit number is four times the sum of the digits. It is also equal to 3 times the product of digits. Find the number.

Solution:
Let the ten’s digit be x and unit’s digit = y
Number 10x + y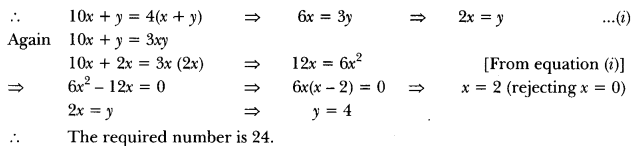

Question:
Find the value of p, for which one root of the quadratic equation px² – 14x + 8 = 0 is 6 times the other.

Solution:
Let the roots of the given equation be a and 6α.
Thus the quadratic equation is (x – a) (x – 6α) = 0
⇒ x² – 7αx + 6α² = 0 …(i)
Given equation can be written as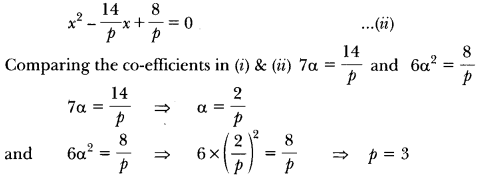

Question: Find the roots of the following quadratic equations by factorisation:
(i) √2x² + 7x + 5√2 = 0 (ii) 2x² – x + 18 = 0

Solution:
(i) We have, √2x² + 7x + 5√2 = 0
= √2x² + 5x + 2x + 5√2 = 0
x(√2x + 5) + √2 (√2x + 5) = 0
= (√2x + 5)(x + √2) = 0
∴ Either √2x + 5 = 0 or x + √2 = 0
∴ x = – 5/√2 or x = -√2
Hence, the roots are – 5/√2 and -√2.
(ii) We have, 2x² – x + 18 = 0

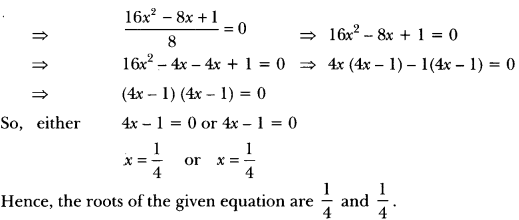
Question: Find the roots of the following quadratic equations, if they exist, by the method of completing the square:
(i) 2x² + x – 4 = 0
(ii) 4x² + 4√3x + 3 = 0

Solution:
(i) We have, 2x² + x – 4 = 0
On dividing both sides by 2, we have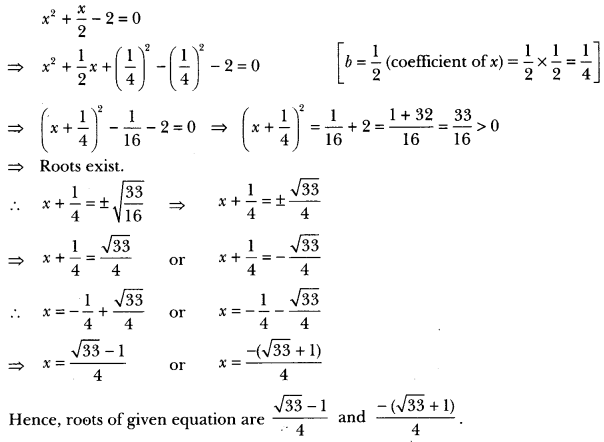

(ii) We have, 4x² + 4√3x + 3 = 0

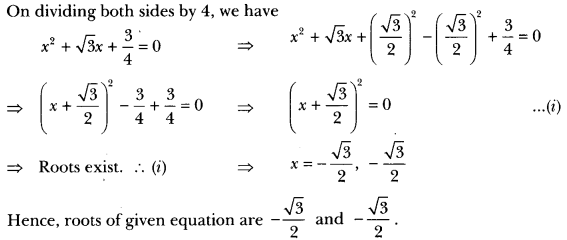
Question:
Find the roots of the following quadratic equations by applying the quadratic formula.
(i) 2x² – 7x + 3 = 0
(ii) 4x² + 4√3x + 3 =0

Solution:
(i) We have, 2x² – 7x + 3 = 0
Here, a = 2, b = -7 and c = 3
Therefore, D = b² – 4ac
⇒ D = (-7)² – 4 × 2 × 3 = 49 – 24 = 25
∵ D > 0, ∴ roots exist.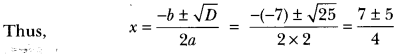


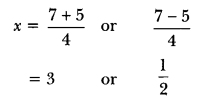
So, the roots of given equation are 3 and 12

(ii) We have, 4x² + 4√3x + 3 = 0
Here, a = 4, b = 4√3 and c = 3
Therefore, D = b² – 4ac = (4√3)² – 4 × 4 × 3 = 48 – 48 = 0
∴ D = 0, roots exist and are equal.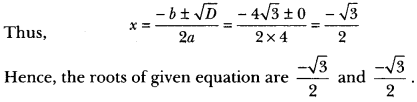

Question:
Using quadratic formula solve the following quadratic equation:
p²x² + (p² – q²) x – q² = 0

Solution:
We have, p²x² + (p² – q²) x – q² = 0
Comparing this equation with ax² + bx + c = 0, we have
a = p², b = p² – q² and c = – q²
∴ D = b² – 4ac
⇒ (p² – q)² – 4 × p² × (-q²)
⇒ (p² – q²)² + 4p²q²
⇒ (p² + q³)² > 0
So, the given equation has real roots given by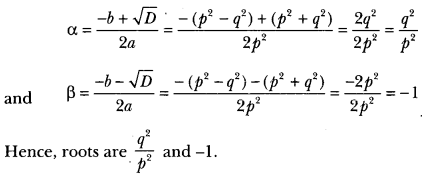

Question:
Find the roots of the following equation:

Solution: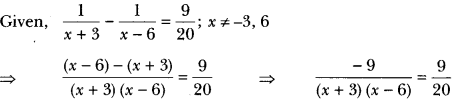

⇒ (x + 3) (x – 6)
⇒ -20 or x² – 3x + 2 = 0
⇒ x² – 2x -x + 2 = 0
⇒ x(x – 2) -1(x – 2) = 0)
⇒ (x – 1) (x – 2) = 0
⇒ x = 1 or x = 2
Both x = 1 and x = 2 are satisfying the given equation. Hence, x = 1, 2 are the solutions of the equation.

Question:
Find the nature of the roots of the following quadratic equations. If the real roots exist, find them:
(i) 3x² – 4√3x + 4 = 0) (ii) 2x² – 6x + 3 = 0

Solution:
(i) We have, 3x² – 4√3x + 4 = 1
Here, a = 3, b = – 4√3 and c = 4
Therefore,
D = b² – 4ac
⇒ (- 4√3)² – 4 × 3 × 4
⇒ 48 – 48 = 0
Hence, the given quadratic equation has real and equal roots.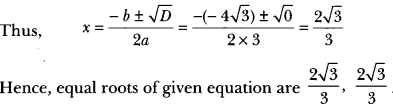

(ii) Wehave, 2x² – 6x + 3 = 0
Here, a = 2, b = -6, c = 3
Therefore, D = b² – 4ac
= (-6)² 4 × 2 × 3 = 36 – 24 = 12 > 0
Hence, given quadratic equation has real and distinct roots.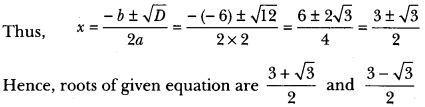

Question: Determine the condition for one root of the quadratic equation ax² + bx + c = 0 to be thrice the other.

Solution:
Let the roots of the given equation be a and 3α.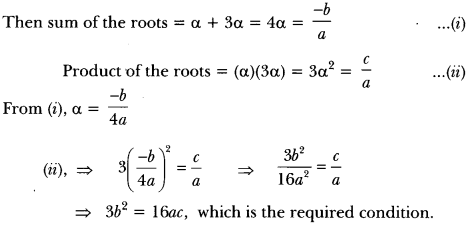

Question:
Solve for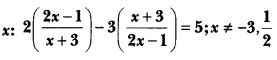

Solution:

⇒ (4x – 2)(2x – 1) – (3x + 9)(x + 3) = 5(x + 3)(2x – 1)
⇒ (8x² – 4x – 4x + 2) – (3x² + 9x + 9x + 27) = 5(2x² – x + 6x – 3)
⇒ 8x² – 8x + 2 – 3x² – 18x – 27 = 10x² + 25x – 15
⇒ 5x² – 26x – 25 = 10x² + 25x – 15
⇒ 5x² + 51x + 10 = 0
⇒ 5x² + 50x + x + 10 = 0
⇒ 5x (x + 10) + 1 (x + 10) = 0
⇒ (5x + 1) (x + 10) = 0
⇒ 5x + 1 = 0 or x + 10 = 0
⇒ x = −15 or x = -10

Question:
Solve the equation

Solution:

⇒ (4 – 3x) (2x + 3) = 5x ⇒ 8x – 6x² + 12 – 9x = 5x
⇒ 6x² + 6x – 12 = 0
⇒ x² + x – 2 = 0
⇒ x² + 2x + x – 2 = 0
⇒ x(x + 2)-1(x + 2) = 0
⇒ (x – 1)(x + 2) = 0
⇒ x – 1 = 0 or x + 2 = 0
⇒ x = 1 or x = -2

Question:
Solve for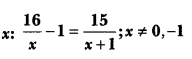

Solution: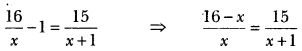

⇒ (16 – x) (x + 1) = 15x
⇒ 16x – x² + 16 – x = 15x
⇒ x² + 15x – 15x – 16 = 0
⇒ x² = 16
⇒ x = ± 4

Question:
Solve for x: + 5x – (a² + a – 6) = 0

Solution:
⇒ x² + 5x – (a² + a – 6) = 0
⇒ x² + 5x – (a? + 3a – 2a – 6) = 0
⇒ x² + 5x – [a(a + 3) -2 (a + 3)] = 0
⇒ x² + 5x – (a – 2) (a + 3) = 0
∴ x² + (a + 3)x – (a – 2) x – (a – 2) (a + 3) = 0
⇒ x[x + (a + 3)]-(a – 2) [X + (a + 3)] = 0
⇒ [{x + (a + 3)} {x – (a – 2)}] = 0
∴ x = -(a + 3) or x = (a -2)
⇒ -(a + 3), (a – 2)
Alternative method
x² + 5x -(a² + a – 6) = 0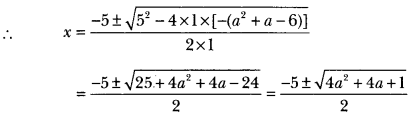

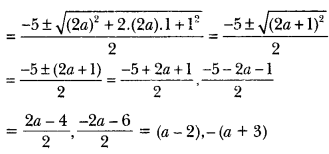
Question:
Solve for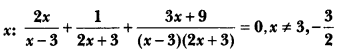

Solution: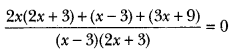

⇒ 2x(2x + 3) + (x – 3) + (3x + 9) = 0
⇒ 4x² + 10x + 6 = 0
⇒ 2x² + 5x + 3 = 0
⇒ (x + 1) (2x + 3) = 0
⇒ x = -1, x = – 32
But x ≠ – 32
∴ x = -1

Extra Questions for Class 10 Maths Chapter 4 Long Answer Type

Question: Using quadratic formula, solve the following equation for x:
abx² + (b2 – ac) x – bc = 0

Solution:
We have, abx² + (b² – ac) x – bc = 0
Here, A = ab, B = b² – ac, C = – bc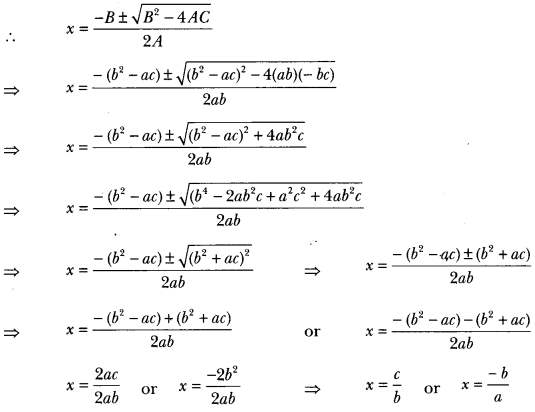

Question:
Find the value of p for which the quadratic equation
(2p + 1)x² – (7p + 2)x + (7p – 3) = 0 has equal roots. Also find these roots.

Solution:
Since the quadratic equation has equal roots, D = 0
i.e., b² – 4ac = 0
In (2p + 1 )x² – (7p + 2)x + (7p – 3) = 0
Here, a = (2p + 1), b = -(7p + 2), c = (7p – 3)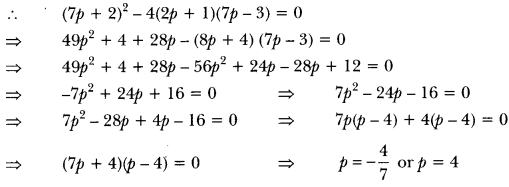

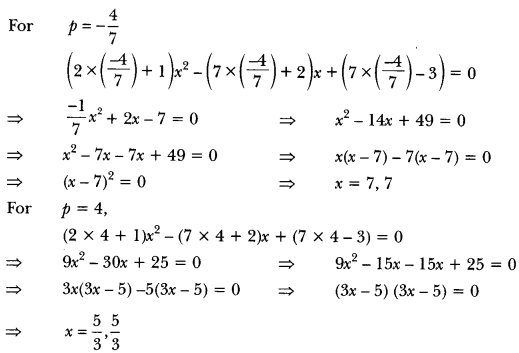
Question:
Solve for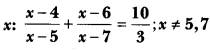

Solution: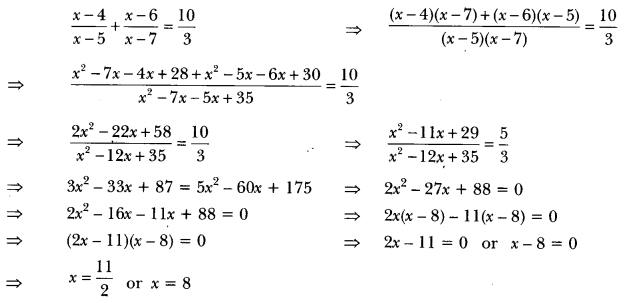

Question:
The sum of the reciprocals of Rehman’s age (in years) 3 years ago and 5 years from now is Find his present age.

Solution:
Let the present age of Rehman be x years.
So, 3 years ago, Rehman’s age = (x – 3) years
And 5 years from now, Rehman’s age = (x + 5) years
Now, according to question, we have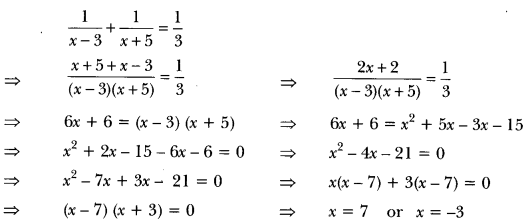

But x ≠ -3 (age cannot be negative)
Therefore, present age of Rehman = 7 years.

Question: A train travels 360 km at a uniform speed. If the speed has been 5 km/h more, it would have taken 1 hour less for the same journey. Find the speed of the train.

Solution:
Let the uniform speed of the train be x km/h.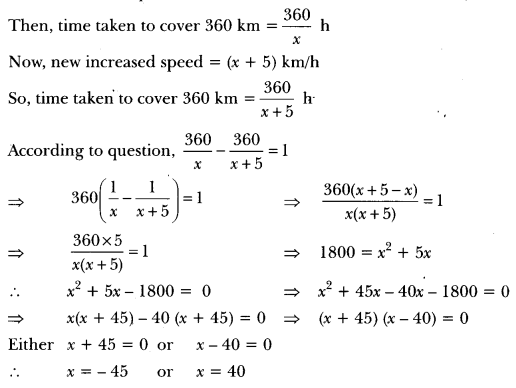

But x cannot be negative, so x ≠ – 45
therefore, x = 40
Hence, the uniform speed of train is 40 km/h.

Question:
The sum of the areas of two squares is 468 m². If the difference of their perimeters is 24 m, find the sides of the two squares.

Solution:
Let x be the length of the side of first square and y be the length of side of the second square.
Then, x² + y² = 468 …(i)
Let x be the length of the side of the bigger square.
4x – 4y = 24
⇒ x – y = 6 or x = y + 6 …(ii)
Putting the value of x in terms of y from equation (ii), in equation (i), we get
(y + 6)² + y² = 468
⇒ y² + 12y + 36 + y² = 468 or 232 + 12y – 432 = 0
⇒ y² + 6y – 216 = 0
⇒ y² + 18y – 12y – 216 = 0
⇒ y(y + 18) – 12(y + 18) = 0
⇒ (y + 18)(y – 12) = 0
Either y + 18 = 0 or y – 12 = 0
⇒ y = -18 or y = 12
But, sides cannot be negative, so y = 12
Therefore, x = 12 + 6 = 18
Hence, sides of two squares are 18 m and 12 m.

Question:
Seven years ago Varun’s age was five times the square of Swati’s age. Three years hence, Swati’s age will be two-fifth of Varun’s age. Find their present ages.

Solution:
Seven years ago, let Swati’s age be x years. Then, seven years ago Varun’s age was 5x² years.
∴ Swati’s present age = (x + 7) years
Varun’s present age = (5x² + 7) years
Three years hence,
Swati’s age = (x + 7 + 3) years = (x + 10) years
Varun’s age (5x² + 7 + 3) years = (5x² + 10) years
According to the question,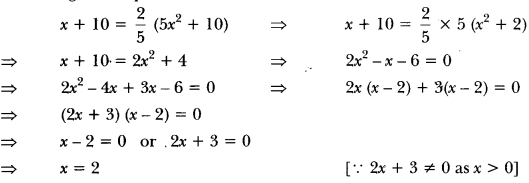

Hence, Swati’s present age = (2 + 7) years = 9 years
and Varun’s present age = (5 × 2² + 7) years = 27 years

Question:
A train covers a distance of 300 km at a uniform speed. If the speed of the train is increased by 5 km/hour, it takes 2 hours less in the journey. Find the original speed of the train.

Solution:
Let the original speed of the train = x km/h.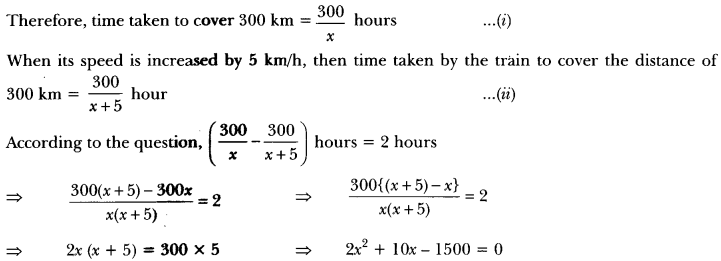


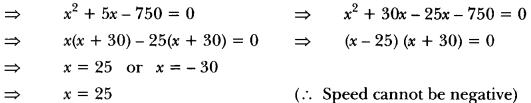
Therefore, the usual speed of the train = 25 km/h.

Question:
A two digit number is such that the product of its digits is 18. When 63 is subtracted from the number, the digits interchange their places. Find the number.

Solution:
Let the digit at tens place be x.

Question: In a class test, the sum of Shefali’s marks in Mathematics and English is 30. Had she got 2 marks more in Mathematics and 3 marks less in English, the product of her marks would have been 210. Find her marks in the two subjects.

Solution:
Let Shefali’s marks in Mathematics be x.
Therefore, Shefali’s marks in English is (30 – x).
Now, according to question,
⇒ (x + 2) (30 – x – 3) = 210
⇒ (x + 2) (27 – x) = 210
⇒ 27x – x² + 54 – 2x = 210
⇒ 25x – x² + 54 – 210 = 0
⇒ 25x – x² – 156 = 0
⇒ -(x² – 25x + 156) = 0
⇒ x² – 25x + 156 = 0
= x² – 13x – 12x + 156 = 0
⇒ x(x – 13) – 12(x – 13) = 0
⇒ (x – 13) (x – 12) = 0
Either x – 13 or x – 12 = 0
∴ x = 13 or x = 12
Therefore, Shefali’s marks in Mathematics = 13
Marks in English = 30 – 13 = 17
or Shefali’s marks in Mathematics = 12
marks in English = 30 – 12 = 18.

Question: Find the positive value(s) of k for which both quadratic equations x² + kx + 64 = 0 and x² – 8x + k = 0 will have real roots.

Solution:
(i) For x² + kx + 64 = 0 to have real roots
⇒ k² – 4(1)(64) ≥ 0 i.e., k² – 256 ≥ 0
⇒ k ≥ ± 16

(ii) For x² – 8x + k = 0 to have real roots
⇒ (-8)² – 4(k) ≥ 0 i.e., 64 – 4k ≥ 0
⇒ k ≤ ± 16
For (i) and (ii) to hold simultaneously k = 16

Question:
Speed of a boat in still water is 15 km/h. It goes 30 km upstream and returns back at the same point in 4 hours 30 minutes. Find the speed of the stream.

Solution:
Let the speed of stream be x km/h.
∴ Speed of boat upstream = (15 – x) km/h.
Speed of boat downstream = (15 + x) km/h.
According to question,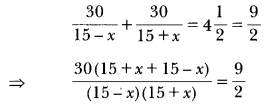

⇒ 30 × 2 × 30 = 9(225 – x²)
⇒ 100 × 2 = 225 – x²
⇒ 200 = 225 – x²
⇒ x² = 25
⇒ x = ±5
⇒ x = 5 (Rejecting – 5)
∴ Speed of stream = 5 km/h

Question:
Ram takes 6 days less than Bhagat to finish a piece of work. If both of them together can finish the work in 4 days, in how many days Bhagat alone can finish the work.

Solution:
Let Bhagat alone can do the work in x number of days
∴ Ram takes (x – 6) number of days
Work done by Bhagat in 1 day = 1x
Work done by Ram in 1 day = 1x−6
According to the question,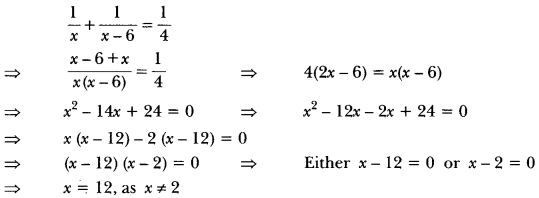

Question: In a rectangular park of dimensions 50 m × 40 m, a rectangular pond is constructed so that the area of grass strip of uniform width surrounding the pond would be 1184 m2. Find the length and breadth of the pond.

Solution: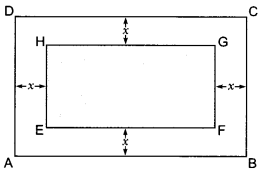

Let ABCD be rectangular lawn and EFGH be rectangular pond. Let x m be the width of grass area, which is same around the pond.
Given, Length of lawn = 50 m
Width of lawn = 40 m
Length of pond = (50 – 2x)m
Breadth of pond = (40 – 2x)m
Also given,
Area of grass surrounding the pond = 1184 m²
⇒ Area of rectangular lawn – Area of pond = 1184 m²
⇒ 50 × 40 – {(50 – 2x) × (40 – 2x)} = 1184
⇒ 2000 – (2000 – 80x – 100x + 4x²) = 1184
⇒ 2000 – 2000 + 180x – 4x² = 1184
⇒ 4x² – 180x + 1184 = 0
⇒ x² – 45x + 296 = 0
⇒ x² – 37x – 8x + 296 = 0
⇒ x(x – 37) – 8(x – 37) = 0
⇒ (x – 37) (x – 8) = 0
⇒ x- 37 = 0 or x – 8 = 0)
⇒ x = 37 or x = 8
x = 37 is not possible as in this case length of pond becomes 50 – 2 × 37 = -24 (not possible) Hence, x = 8 is acceptable
∴ Length of pond = 50 – 2 × 8 = 34 m
Breadth of pond = 40 – 2 × 8 = 24 m

Question:
A car covers a distance of 2592 km with uniform speed. The number of hours taken for the journey is one-half the number representing the speed, in km/hour. Find the time taken to cover the distance.

Solution:
Let speed of the car be x km/h
According to question
Time taken = x2 h.

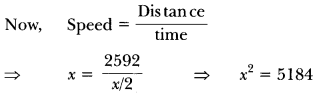
⇒ x = 72 km/h [Taking square root both sides]
∴ Time taken = x/2 = 36 hours.