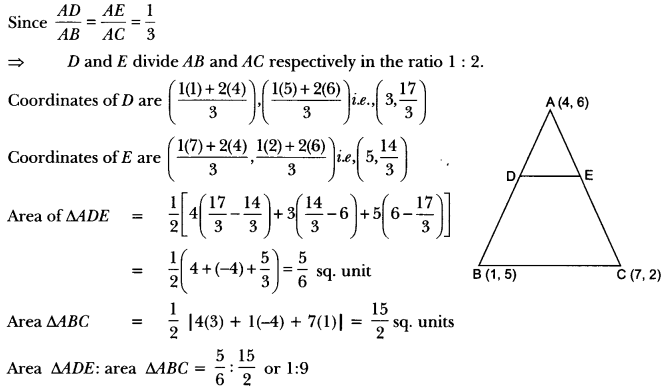We have provided you with Extra and Important Questions from Class 10 Maths Chapter 7 Coordinate Geometry. This Extra and Important Questions will help you to score 100% in your Board Exams. These extra questions will be helpful to revise the important topics and concepts.

Coordinate Geometry Class 10 Important Questions with Answers Maths Chapter 7

Extra Questions for Class 10 Maths Chapter 7 Very Short Answer Type

Question:If the centroid of triangle formed by points P (a, b), Q (b, c) and R (c, a) is at the origin, what is the value of a + b + c?

Solution:

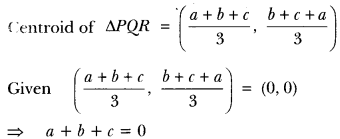
Question: AOBC is a rectangle whose three vertices are A (0, 3), 0 (0, 0) and B (5, 0). Find the length of its diagonal.

Solution:

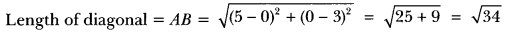
Question:Find the value of a, so that the point (3, a) lie on the line 2x – 3y = 5.

Solution:Since (3, a) lies on the line 2x – 3y = 5
Then 2(3) – 3(a) = 5
– 3a = 5 – 6
– 3a = -1
⇒ a = 1/3

Question:Find distance between the points (0, 5) and (-5, 0).

Solution:

Here x₁ = 0, y₁ = 5, x₂ = -5 and y₂ = 0)

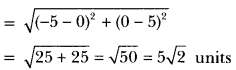
Question:Find the distance of the point (-6,8) from the origin.

Solution:

Here x₁ = -6, y₁ = 8
x₂ = 0, y₂ = 0

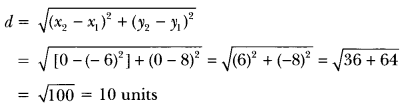
Question:If the distance between the points (4, k) and (1, 0) is 5, then what can be the possible values of k?

Solution:

Using distance formula

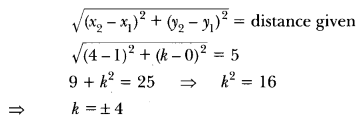
Question:If the points A (1, 2), B (0, 0) and C (a, b) are collinear, then what is the relation between a and b?

Solution:

Points A, B and C are collinear
⇒ 1(0 – b) + 0 (b – 2) + a(2 – 0) = 0
⇒ -b + 2a = 0 or 2a = b

Question:Write the coordinates of a point on x-axis which is equidistant from the points (-3, 4) and (2, 5).

Solution:

Let the required point be (x, 0).
Since, (x, 0) is equidistant from the points (-3, 4) and (2, 5) .

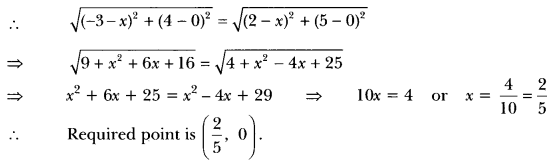
Question:Find the values of x for which the distance between the points P (2, -3) and Q (x, 5) is 10.

Solution:

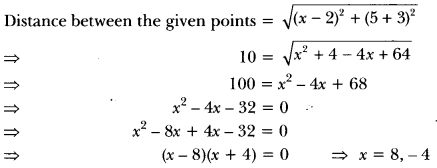
Question:What is the distance between the points (10 cos 30°, 0) and (0, 10 cos 60°)?

Solution:

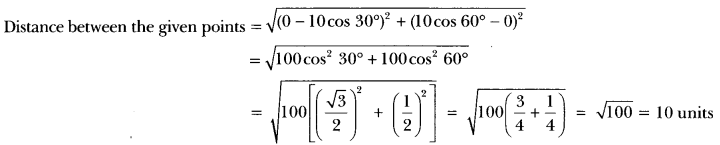
Extra Questions for Class 10 Maths Chapter 7 Short Answer Type

Question:In Fig. 6.8, if A(-1, 3), B(1, -1) and C (5, 1) are the vertices of a triangle ABC, what is the length of the median through vertex A?

Solution:

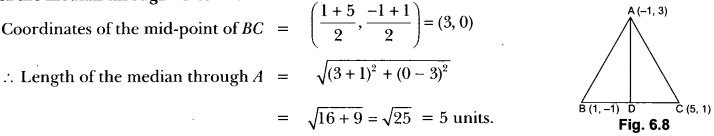
Question:Find the ratio in which the line segment joining the points P (3, -6) and Q (5,3) is divided by the x-axis.

Solution:

Let the required ratio be λ : 1

Given that this point lies on the x-axis

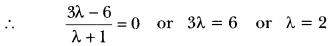
Thus, the required ratio is 2 : 1.

Question:Point P (5, -3) is one of the two points of trisection of the line segment joining the points A (7, -2) and B (1, -5). State true or false and justify your answer.

Solution:

Points of trisection of line segment AB are given by

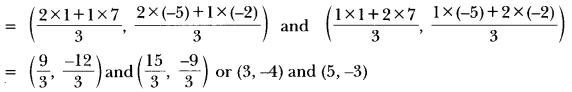
∴ Given statement is true.

Question:Show that ∆ABC, where A(-2, 0), B(2, 0), C(0, 2) and APQR where P(-4, 0), Q(4, 0), R(0,4) are similar triangles.
OR
Show that ∆ABC with vertices A(-2, 0), B(0, 2) and C(2, 0) is similar to ∆DEF with vertices D(-4, 0), F(4,0) and E(0, 4).
[∆PQR is replaced by ∆DEF]

Solution:

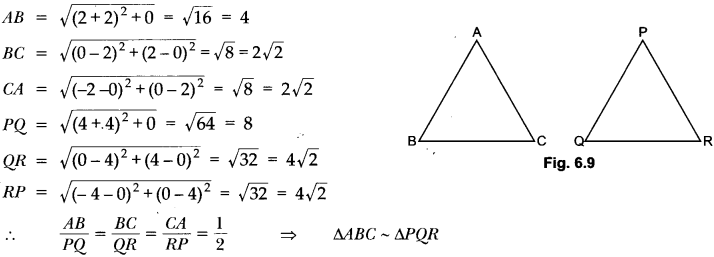
Question:Point P (0, 2) is the point of intersection of y-axis and perpendicular bisector of line segment joining the points, A (-1, 1) and B (3, 3). State true or false and justify your answer.

Solution:

The point P (0, 2) lies on y-axis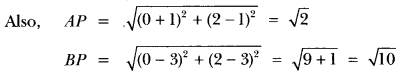

AP ≠ BP
∴ P(0, 2) does not lie on the perpendicular bisector of AB. So, given statement is false.

Question:Determine, if the points (1, 5), (2, 3) and (-2, -11) are collinear.

Solution:

Let A (1, 5), B (2, 3) and C (-2, -11) be the given points. Then we have

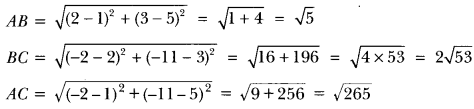
Clearly, AB + BC ≠ AC
∴ A, B, C are not collinear.

Question:Find the distance between the following pairs of points:
(i) (-5, 7), (-1, 3)
(ii) (a, b), (-a, -b)

Solution:

(i) Let two given points be A (-5, 7) and B (-1, 3).
Thus, we have x₁ = -5 and x₂ = -1
y₁ = 7 and y₂ = 3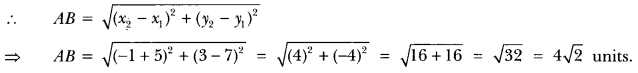

(ii) Let two given points be A (a,b) and B(-a, -b)
Here, x₁ = a and x₂ = -a; y₁ = b and y₂ = -b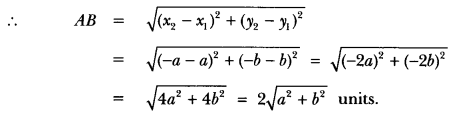

Question:Name the type of quadrilateral formed, if any, by the following points, and give reasons for
your answer: (i) (-1, -2), (1, 0), (- 1, 2), (-3, 0) (ii) (4, 5), (7, 6), (4, 3), (1, 2)

Solution:

(i) Let A(-1, -2), B(1, 0), C(-1, 2) and D(-3, 0) be the four given points.
Then, using distance formula, we have,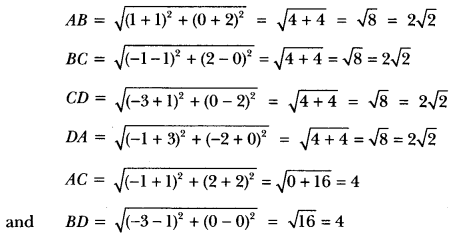

Hence, four sides of quadrilateral are equal and diagonals AC and BD are also equal.
∴ Quadrilateral ABCD is a square.

(ii) Let A (4, 5), B (7, 6), C (4, 3) and D (1, 2) be the given points. Then,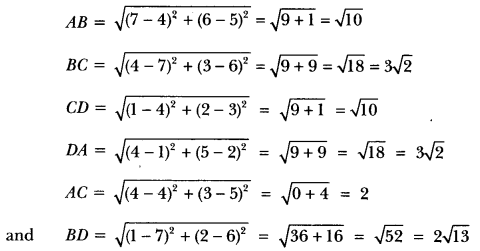

∴ ABCD is a parallelogram.

Question:Find the value of y for which the distance between the points P(2, -3) and Q(10, y) is 10 units.
OR
A line segment is of length 10 units. If the coordinates of its one end are (2, -3) and the abscissa of the other end is 10, find its ordinate.

Solution:

We have, PQ = 10

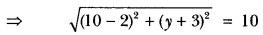
Squaring both sides, we have
⇒ (8)² + (y + 3)² = 100
⇒ (y + 3)² = 100 – 64
⇒ (y + 3)² = 36 or y + 3 ± 16
⇒ y + 3 = 6, y + 3 = -6 or y = 3, y = -9
Hence, values of y are – 9 and 3.

Question:If Q(0, 1) is equidistant from P(5,-3) and R(x, 6) find the value of x. Also, find the distances of QR and PR.

Solution:

Since, point Q(0, 1) is equidistant from P(5, -3) and R(x, 6).
Therefore, QP = QR
Squaring both sides, we have, Qp² = QR²
⇒ (5 – 0)² + (-3 -1)² = (x – 0)² + (6 – 1)²
25 + 16 = x² + 25
x² = 16
∴ x = ±4
Thus, R is (4, 6) or (-4, 6).

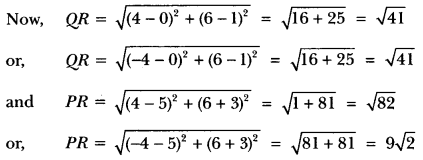
Question:Find a relation between x and y such that the point (x, y) is equidistant from the point (3,6) and (-3, 4).

Solution:Let P(x, y) be equidistant from the points A(3, 6) and B(-3, 4)
i.e., PA = PB
Squaring both sides, we get
AP² = BP²
⇒ (x – 3)² + (y – 6)² = (x + 3)² + (1 – 4)²
⇒ x² – 6x + 9 + y² – 12y + 36 = x² + 6x + 9 +y² – 8y + 16
⇒ -12x – 4y + 20 = 0
⇒ 3x + y – 5 = 0, which is the required relation.

Question:Find the coordinates of the point which divides the line joining of (- 1, 7) and (4, – 3) in the ratio 2 : 3.

Solution:

Let P(x, y) be the required point. Thus, we have

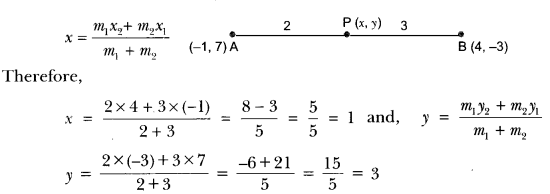
So, the coordinates of P are (1, 3).

Extra Questions for Class 10 Maths Chapter 7 Long Answer Type

Question:Find the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are (0, -1), (2, 1) and (0, 3). Find the ratio of this area to the area of the given triangle.

Answer:

Let A (x₁, y₁) = (0, -1), B (x₂, y₂) = (2, 1), C (x₃, y₃) = (0, 3) be the vertices of ∆ABC.
Now, let P, Q, R be the mid-points of BC, CA and AB, respectively.
So, coordinates of P, Q, R are

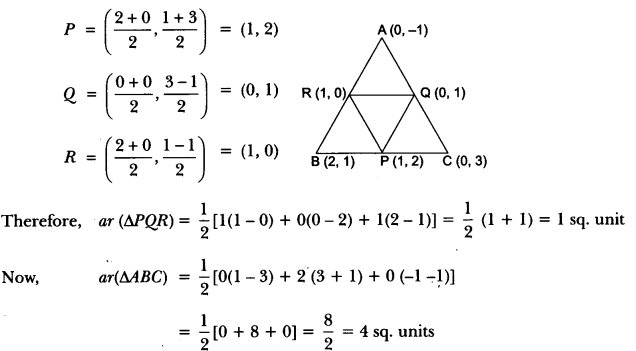
Ratio of ar (∆PQR) to the ar (∆ABC) = 1 : 4.

Question:Find the area of the quadrilateral whose vertices, taken in order, are (-4, -2), (-3, -5), (3, -2) and (2, 3).

Answer: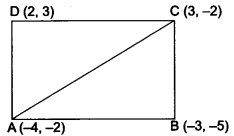

Let A(4, -2), B(-3, -5), C(3, -2) and D(2, 3) be the vertices of the quadrilateral ABCD.
Now, area of quadrilateral ABCD
= area of ∆ABC + area of ∆ADC

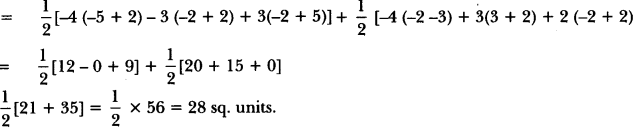
Question:A median of a triangle divides it into two triangles of equal areas. Verify this result for ∆ABC whose vertices are A (4,-6), B (3, -2) and C (5, 2).

Answer:

Since AD is the median of ∆ABC, therefore, D is the mid-point of BC.

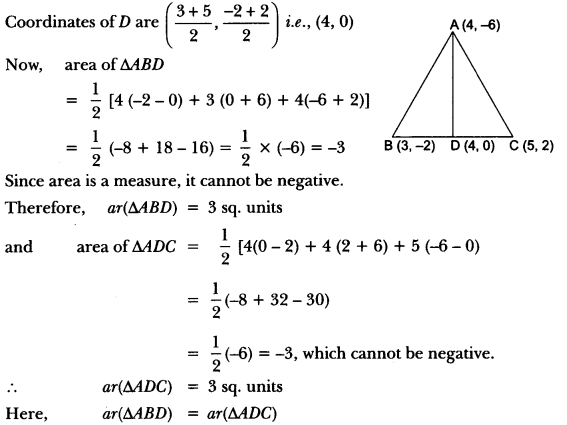
Hence, the median divides it into two triangles of equal areas.

Question:Find the ratio in which the point P (x, 2), divides the line segment joining the points A (12, 5) and B (4, -3). Also find the value of x.

Answer:

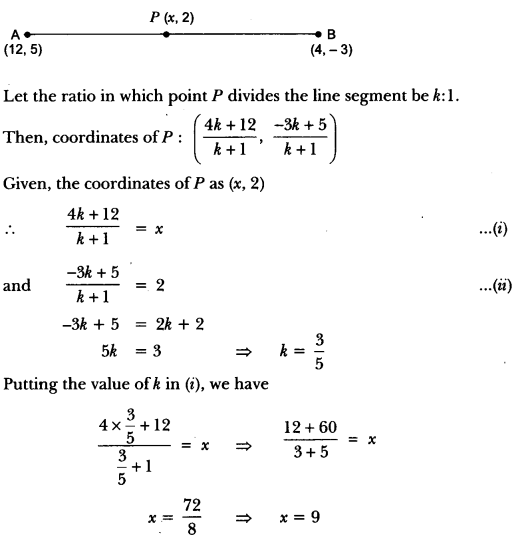
The ratio in which p divides the line segment is 3/5, i.e., 3 : 5.

Question:If A (4, 2), B (7, 6) and C (1, 4) are the vertices of a ∆ABC and AD is its median, prove that the median AD divides into two triangles of equal areas.

Answer:

Given: AD is the median on BC.
⇒ BD = DC
The coordinates of midpoint D are given by.

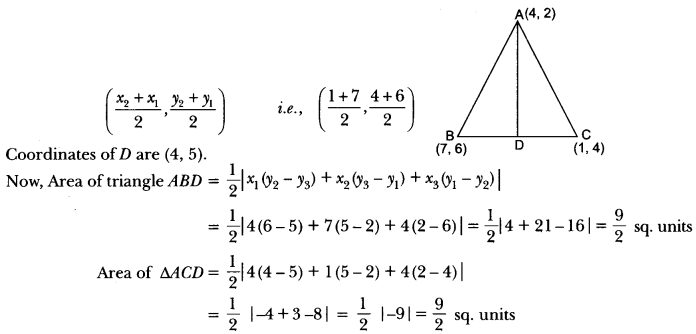
Hence, AD divides ∆ABC into two equal areas.

Question:If the point A (2, -4) is equidistant from P (3, 8) and Q (-10, y), find the values of y. Also find distance PQ.

Answer:

Given points are A(2, 4), P(3, 8) and Q(-10, y)
According to the question,
PA = QA

Question:The base BC of an equilateral triangle ABC lies on y-axis. The coordinates of point Care (0, -3). The origin is the mid-point of the base. Find the coordinates of the points A and B. Also find the coordinates of another point D such that BACD is a rhombus.

Answer:

∵ O is the mid-point of the base BC.
∴ Coordinates of point B are (0, 3). So,
BC = 6 units Let the coordinates of point A be (x, 0).
Using distance formula,

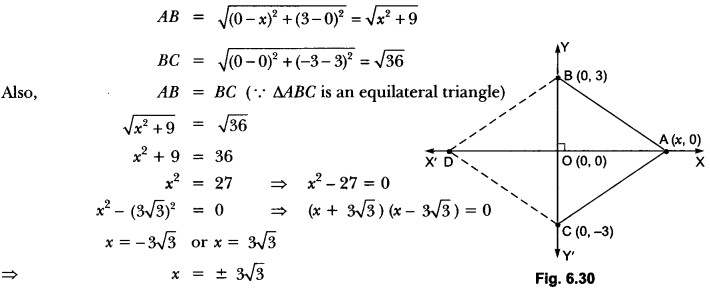
∴ Coordinates of point A = (x, 0) = (3√3, 0)
Since BACD is a rhombus.
∴ AB = AC = CD = DB
∴ Coordinates of point D = (-3√3, 0).

Question:In Fig. 6.32, the vertices of ∆ABC are A(4, 6), B(1, 5) and C(7, 2). A line-segment DE is drawn to intersect the sides AB and AC at D and E respectively such that \(\frac{A D}{A B}=\frac{A E}{A C}=\frac{1}{3}\) Calculate the area of ∆ADE and compare it with area of ∆ABC.

Answer:

\