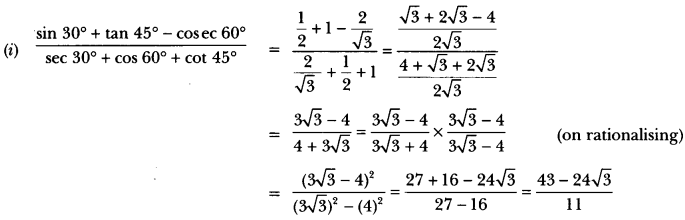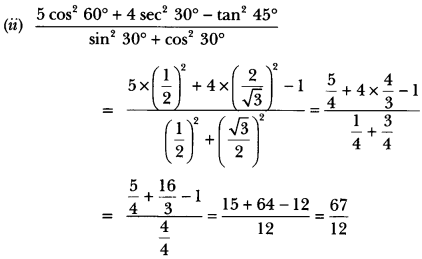We have provided you with Extra and Important Questions from Class 10 Maths Chapter 8 Introduction to Trigonometry. This Extra and Important Questions will help you to score 100% in your Board Exams. These extra questions will be helpful to revise the important topics and concepts.

Introduction to Trigonometry Class 10 Important Questions with Answers Maths Chapter 8

Extra Questions for Class 10 Maths Chapter 8 Very Short Answer Type

Question:If sin θ = cos θ, then find the value of 2 tan θ + cos² θ.

Solution:

sin θ = cos θ (Given)
It means value of θ = 45°
Now, 2 tan θ + cos² θ = 2 tan 45° + cos² 45°

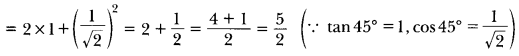
Question:If sin (x – 20)° = cos (3x – 10)°, then find the value of x.

Solution:

sin (x – 20)° = cos (3x – 10)°
⇒ cos [90° – (x – 20)°] = cos (3x – 10)°
By comparing the coefficient
90° – x° + 20° = 3x° – 10° = 110° + 10° = 3x° + x°
120° = 4x°
⇒ 120∘/4 = 30°

Question:If x = a cos θ, y = b sin θ, then find the value of b²x² + a²y² – a²b².

Solution:Given x = acos θ, y = b sin θ
b²x² + a²y² – a²b² = b²(acos θ)² + a²(b sin θ)² – a²b²
= a²b² cos²θ + a²b² sin² θ – a²b² = a²b² (sin² θ + cos² θ) – a²b²
= a²b² – a²b² = θ (∵ sin² θ + cos² θ = 1)

Question:If tan A = cot B, prove that A + B = 90°.

Solution:We have
tan A = cot B
⇒ tan A = tan (90° – B)
A = 90° – B
[∵ Both A and B are acute angles]
⇒ A + B = 90°

Question:In a ∆ABC, if ∠C = 90°, prove that sin² A + sin² B = 1.

Solution:Since ∠C = 90°
∴ ∠A + ∠B = 180° – ∠C = 90°
Now, sin² A + sin² B = sin² A + sin² (90° – A) = sin² A + cos² A = 1

Question:If sec 4A = cosec (A – 20°) where 4 A is an acute angle, find the value of A.

Solution:

We have
sec 4 A = cosec (A – 20°)
⇒ cosec (90° – 4 A) = cosec (A – 20°)
∴ 90° – 4 A = A – 20°
⇒ 90° + 20° = A + 4 A
⇒ 110° = 5 A
∴ A = 110/5 = 22°

Question:If sin A = 3/4, calculate cos A and tan A.

Solution:

Let us first draw a right ∆ABC in which ∠C = 90°.
Now, we know that

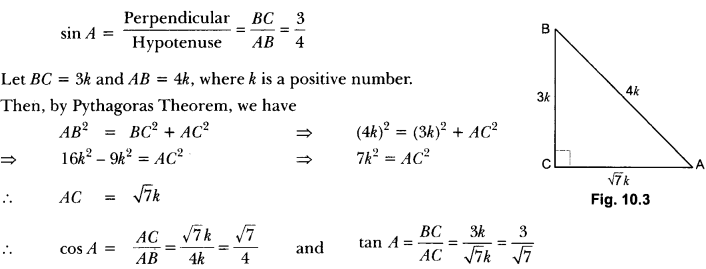
Question:Given 15 cot A = 8, find sin A and sec A.

Solution:

Let us first draw a right ∆ABC in which ∠B = 90°.
Now, we have, 15 cot A = 8

Question:If sin θ + cos θ = √3 , then prove that tan θ + cot θ = 1.

Solution:

sin θ + cos θ = √3
⇒ (sin θ + cos θ)² = 3
⇒ sin² θ + cos² θ + 2 sin θ cos θ = 3
⇒ 2 sin cos θ = 2 (∵ sin² θ + cos² θ = 1)
⇒ sin θ. cos θ = 1 = sin² θ + cos² θ

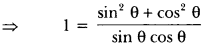
⇒ 1 = tan θ + cot θ = 1
Therefore tan θ + cot θ = 1

Question:

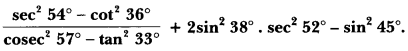
Solution:

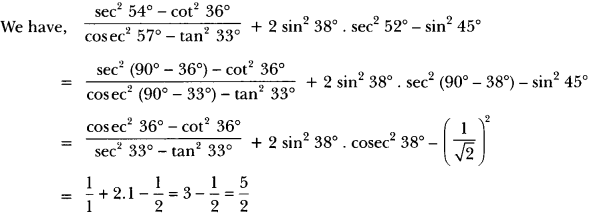
Extra Questions for Class 10 Maths Chapter 8 Short Answer Type

Question:

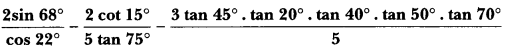
Solution:

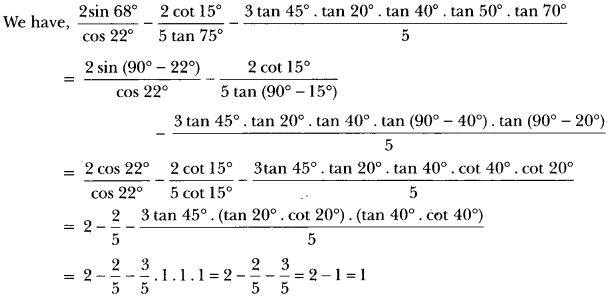
Question:

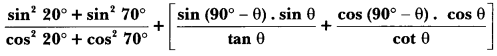
Solution:

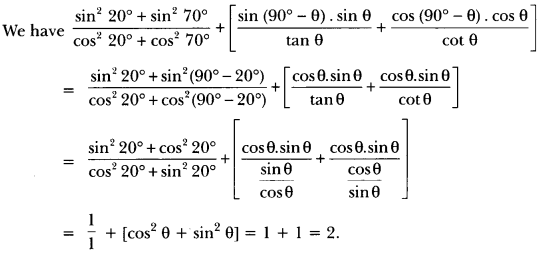
Question:Evaluate: sin 25° cos 65° + cos 25° sin 65°.

Solution:sin 25°. cos 65° + cos 25° . sin 65°
= sin (90° – 65°). cos 65° + cos (90° – 65°). sin 65°
= cos 65° . cos 65° + sin 65°. sin 65°
= cos² 65° + sin² 65° = 1.

Question:If sin 30 = cos (θ – 6°) where 30 and (θ – 6°) are both acute angles, find the value of θ.

Solution:

According to question:
sin 3θ = cos (θ – 6°)
cos (90° – 30) = cos (θ – 6°) [∵ cos (90° – θ ) = sin θ]
90° – 3θ = θ – 6° [comparing the angles)
= 4θ = 90° + 6° = 96°
θ = 96/4 = 24°
Hence, θ = 24°

Question:

Find an acute angle θ, when

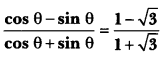
Solution:

On comparing we get
⇒ tan θ = √3
⇒ tan θ = tan 60°
= θ = 60°

Question:

Prove that

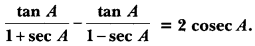
Solution:

n:

Question:

Prove that

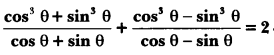
Solution:

We have,

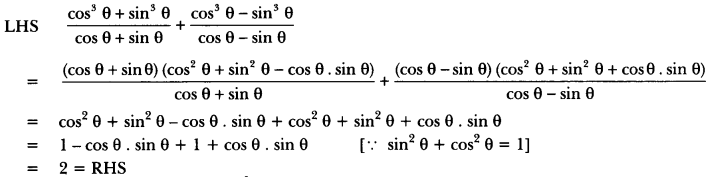
Question:

Prove that:

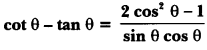
Solution:

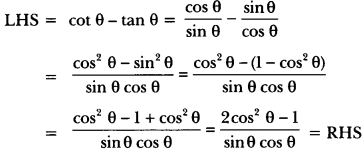
Question:

Prove that:

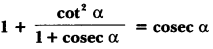
Solution:

Question:

Evaluate the following:

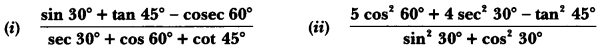
Solution:

n:

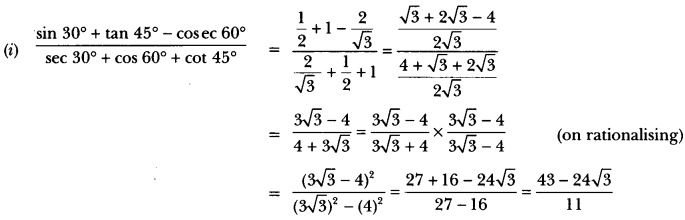
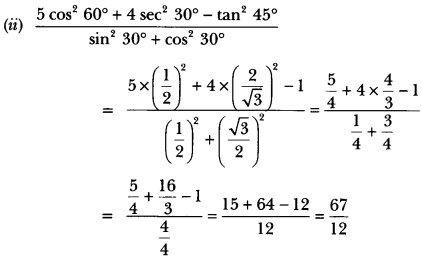
Extra Questions for Class 10 Maths Chapter 8 Long Answer Type

Question:

Prove that:

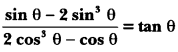
Solution:

n:

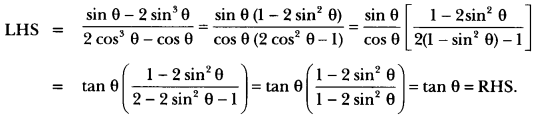
Question:Prove that: (sin A + cosec A)² + (cos A + sec A)² = 7 + tan² A + cot²A.

Solution:LHS = (sin A + cosec A)² + (cos A + sec A)²
= sin² A + coses² A + 2sin A . cosec A + cos² A + sec² A + 2 cos A . sec A
= (sin² A + coses² A + 2) + (cos² A + sec² A + 2) [sin A. cosec A = 1]
= (sin² A + cos² A) + (coses² A + sec² A) + 4 [cos A. sec A = 1]
= 1 + 1 + cot²A + 1 + tan² A + 4
= 7 + tan² A + cot² A = RHS [∵ 1 + cot²A = coses² A and 1 + tan² A = sec² A]

Question:

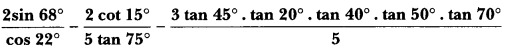
Solution:

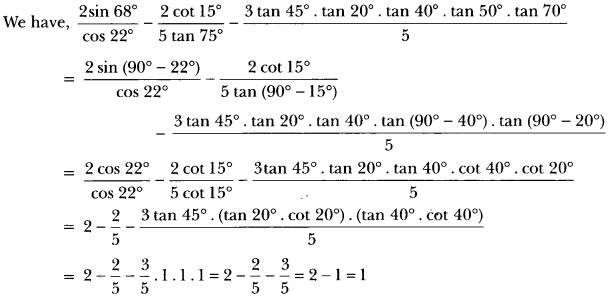
Question:

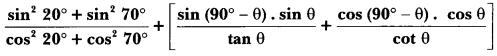
Solution:

Question: Prove that

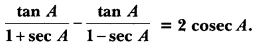
Solution:

Question: Evaluate the following:

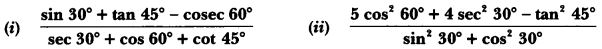
Solution: