We have provided you with Extra and Important Questions from Class 10 Maths Chapter 9 Some Applications of Trigonometry. This Extra and Important Questions will help you to score 100% in your Board Exams. These extra questions will be helpful to revise the important topics and concepts.

Some Applications of Trigonometry Class 10 Important Questions with Answers Maths Chapter 9

Extra Questions for Class 10 Maths Chapter 9 Very Short Answer Type

Question:

If a man standing on a platform, 3 metres above the surface of a lake observes a cloud and its reflection in the lake, then the angle of elevation of the cloud is equal to the angle of depression of its reflection.

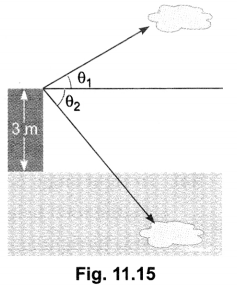
Solution:False, θ₁ ≠ θ₁ (Fig. 11.15)

Question:Find the angle of elevation of the sun when the shadow of a pole h m high is √3 h m long.

Solution:

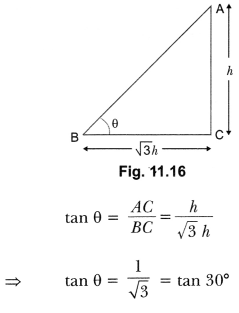
In ∆ABC

θ = 30°

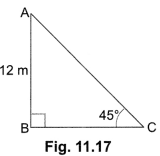
Question:The height of a tower is 12 m. What is the length of its shadow when 10 Sun’s altitude is 45°?

Solution:

Let AB be the tower [Fig. 11.17].
Then, ∠C = 45°, AB = 12 m

photo

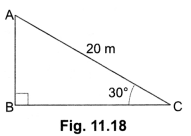
Question:A circus artist is climbing a 20 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole, if the angle made by the rope with the ground level is 30° [Fig. 11.18].

Solution:
Let AB be the vertical pole and AC be the long rope tied to point C.
In right ∆ABC, we have

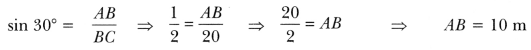
Therefore, height of the pole is 10 m.

Question:The angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower, is 30°. Find the height of the tower.

Solution:

Let BC be the tower whose height is h metres and A be the point at a distance of 30 m from the
foot of the tower. The angle of elevation of the top of the tower from point A is given to be 30°.
Now, in right angle ∆CBA we have,

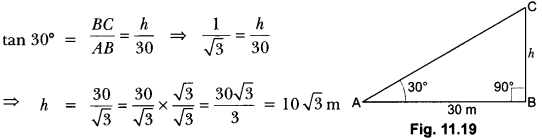
Hence, the height of the tower is 10 √3 m.

Question:The angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is 6 m.

Solution:

n:

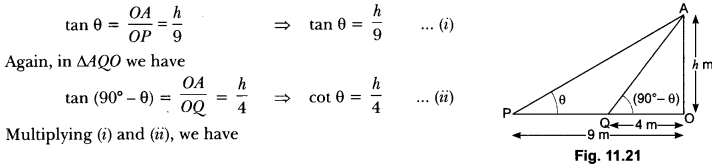
Let OA be the tower of height h metre and P, l be the two points at distance of 9 m and 4 m respectively from the base of the tower.
Now, we have OP = 9 m, OQ = 4 m,
Let ∠APO = θ, ∠AQO = (90° – θ)
and OA = h metre (Fig. 11.21)
Now, in ∆POA, we have

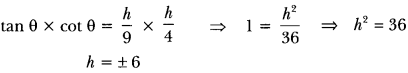
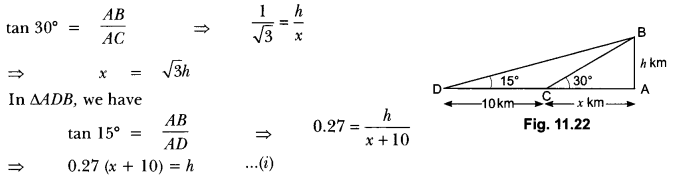
Height cannot be negative.
Hence, the height of the tower is 6 metre.

Extra Questions for Class 10 Maths Chapter 9 Short Answer Type

Question:Determine the height of a mountain if the elevation of its top at an unknown distance from the base is 30° and at a distance 10 km further off from the mountain, along the same line, the angle of elevation is 15o. (Use tan 15° = 0.27)

Solution:

Let AB be the mountain of height h kilometres. Let C be a point at a distance of x km, from the base of the mountain such that the angle of elevation of the top at C is 30°. Let D be a point at a distance of 10 km from C such that angle of elevation at D is of 15°.
In MBC (Fig. 11.22), we have

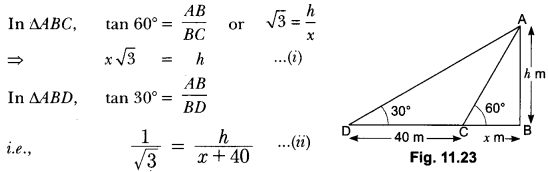
Substituting x = √3h in equation (i), we get
⇒ 0.27 ( √3h + 10) = h
= 0.27 × √3h + 0.27 × 10 = h
⇒ 2.7 = h – 0.27 × √3h
⇒ 27 = h (1 – 0.27 × √3)
⇒ 27 = h (1 – 0.46)
⇒ h = 2.7/0.54 = 5
Hence, the height of the mountain is 5 km.

Question:The shadow of a tower standing on a level ground is found to be 40 m longer when the Sun’s altitude is 30° than when it is 60°. Find the height of the tower.

Solution:

In Fig. 11.23, AB is the tower and BC is the length of the shadow when the Sun’s altitude is 60°, i.e., the angle of elevation of the top of the tower from the tip of the shadow is 60° and DB is the length of the shadow, when the angle of elevation is 30°.
Now, let AB be h m and BC be x m.
According to the question, DB is 40 m longer than BC.
So, BD = (40 + x) m
Now, we have two right triangles ABC and ABD.

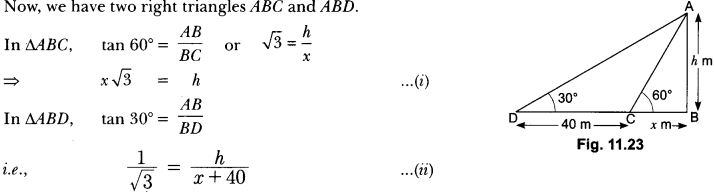
Using (i) in (ii), we get (x √3 ) √3 = x + 40, i.e., 3x = x + 40
i.e., x = 20
So, h = 20 √3 [From (i)]
Therefore, the height of the tower is 20 √3 m.

Question:From a point P on the ground, the angle of elevation of the top of a 10m tall building is 30°. A flag is hosted at the top of the building and the angle of elevation of the top of the flagstaff from P is 45o. Find the length of the flagstaff and the distance of the building from the point P. (You may take √3 = 1.732).

Solution:

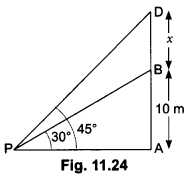
In Fig. 11.24, AB denotes the height of the building, BD the flagstaff and P the given point. Note that there are two right triangles PAB and PAD. We are required to find the length of the flagstaff, i.e., BD and the distance of the building from the point P, i.e., PA.Since, we know the height of the building AB, we will first consider the right ∆PAB.

i.e., x = 100(√3 – 1) = 7.32 So, the length of the flagstaff is 7.32 m.

Question:A tree breaks due to storm and the broken part bends, so that the top of the tree touches the ground making an angle 30° with it. The distance between the foot of the tree to the point where the top touches the ground is 8 m. Find the height of the tree.

Solution:

In right angle ∆ABC, AC is the broken part of the tree (Fig. 11.20).
So, the total height of tree = (AB + AC)
Now in right angle ∆ABC,

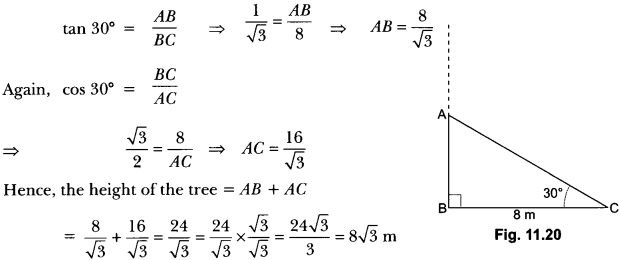
Question:The angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is 6 m.

Solution:

n:

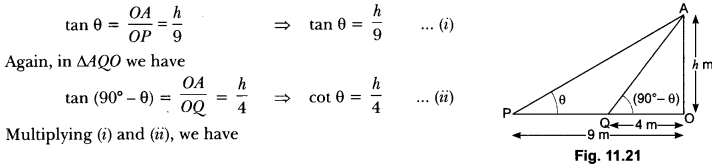
Let OA be the tower of height h metre and P, l be the two points at distance of 9 m and 4 m respectively from the base of the tower.
Now, we have OP = 9 m, OQ = 4 m,
Let ∠APO = θ, ∠AQO = (90° – θ)
and OA = h metre (Fig. 11.21)
Now, in ∆POA, we have

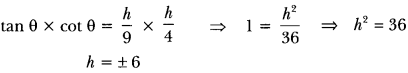
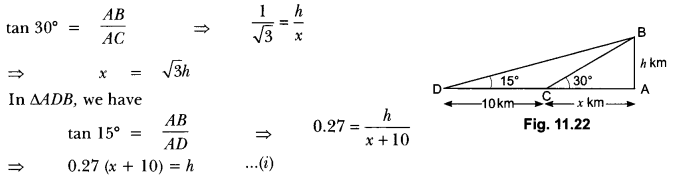
Height cannot be negative.
Hence, the height of the tower is 6 metre.

Question:A kite is flying at a height of 60 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. Find the length of the string, assuming that there is no slack in the string.

Solution:

Let AB be the horizontal ground and K be the position of the kite and its height from the ground is 60 m and let length of string AK be x m. (Fig. 11.26)
∠KAB = 60°
Now, in right angle ∆ABK we have

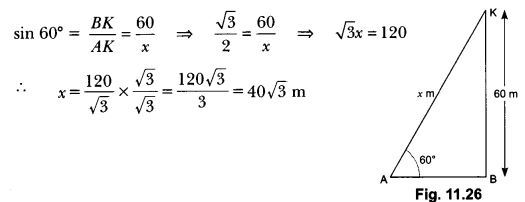
So, the length of string is 40 √3 m.

Question : A 1.5 m tall boy is standing at some distance from a 30 m tall building. The angle of elevation from his eyes to the top of the building increases from 30° to 60° as he walks towards the building. Find the distance he walked towards the building.

Solution:

Let AB be the building and PQ be the initial position of the boy (Fig. 11.27) such that
∠APR = 30°
and AB = 30 m
Now, let the new position of the boy be P’Q’ at a distance QQ’.
Here, ∠AP’R = 60°
Now, in ∆ARP, we have

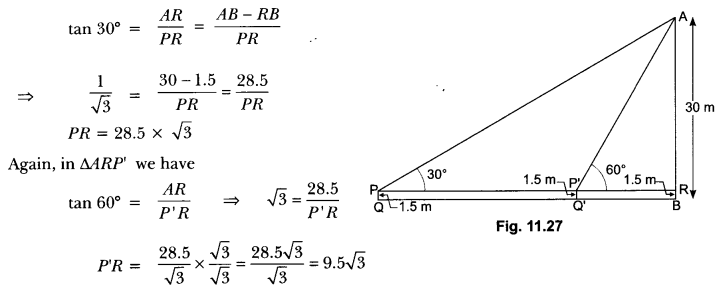
Therefore, required distance, QQ = PP’ = PR – P’R
= 28.5 √3 – 9.5 √3 = 19√3
Hence, distance walked by the boy is 19√3 m.

Question:From a point on a bridge across a river, the angles of depression of the banks on opposite sides of the river are 30° and 45° respectively. If the bridge is at a height of 3 m from the banks, find
the width of the river.

Solution:

In Fig. 11.28, A and B represent points on the bank on opposite sides of the river, so that AB is the width of the river. P is a point on the bridge at a height of 3 m, i.e., DP = 3m. We are interested to determine the width of the river, which is the length of the side AB of the ∆APB.
In right ∆ADP, ∠A = 30°

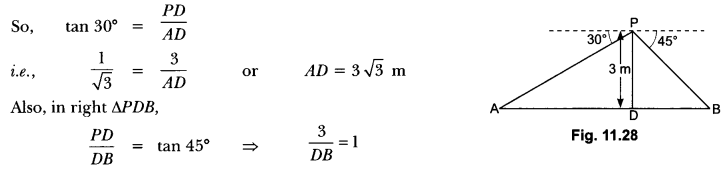
∴ DB = 3m
Now, AB = BD + AD = 3 + 3 √3 = 3 (1 + √3) m
Therefore, the width of the river is 3(√3 + 1) m.

Question:Two ships are there in the sea on either side of a light house in such a way that the ships and the light house are in the same straight line. The angles of depression of two ships as observed from the top of the light house are 60° and 45°. If the height of the light house is 200 m, find the distance between the two ships. (Use √3 = 1.73]

Solution:

Let the distance between the two ships be d.
Let the distance of one ship from the light house be x metres. Then, the distance of the other ship from the light house will be (d – x) metres.

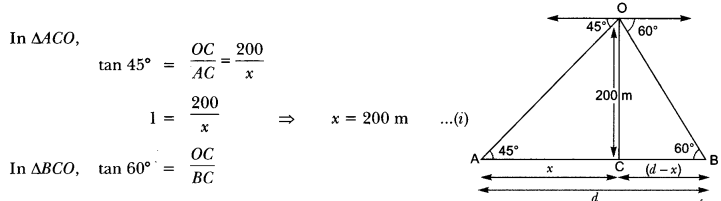
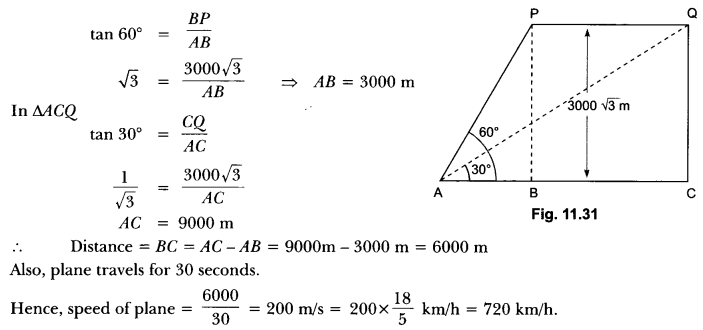
Question:The angle of elevation of an aeroplane from a point on the ground is 60°. After a flight of 30 seconds the angle of elevation becomes 30°. If the aeroplane is flying at a constant height of 3000 √3 m, find the speed of the aeroplane.

Solution:

Let A be point of observation and P and Q be positions of the plane. Let ABC be the line through A and it is given that angles of elevation from point A to two positions P and Q are 60° and 30°.
∠PAB = 60°, ∠QAB = 30°
Height = 3000 √3 m
So, in ∆ABP, we have

Extra Questions for Class 10 Maths Chapter 9 Long Answer Type

Question:From a point on the ground, the angles of elevation of the bottom and the top of a transmission tower fixed at the top of a 20 m high building are 45° and 60°, respectively. Find the height of the tower.

Solution:

Let AB be a building of height 20 m and BC be the transmission tower of height x m and D be any point on the ground (Fig. 11.36).
Here, ∠BDA = 45° and ∠ADC = 60°
Now, in ∆ADC, we have

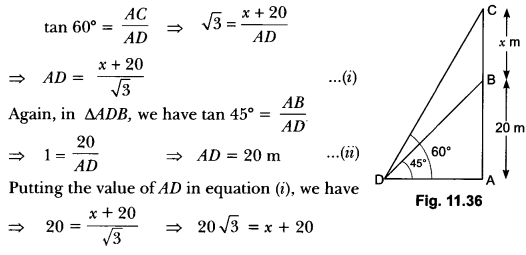
⇒ x = 20√3 – 20 = 20 (√3 – 1) = 20 (1.732 – 1) = 20 × 0.732 = 14.64 m
Hence, the height of tower is 14.64 m.

Question:A statue, 1.6 m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60° and from the same point, the angle of elevation of the bottom of the pedestal is 45°. Find the height of the pedestal.

Solution:

Let AB be the pedestal of height h metres and BC be the statue of height 1.6 m (Fig. 11.37).
Let D be any point on the ground such that,
∠BDA = 45° and ∠CDA = 60°
Now, in ∆BDA, we have

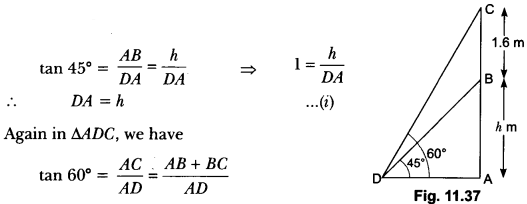
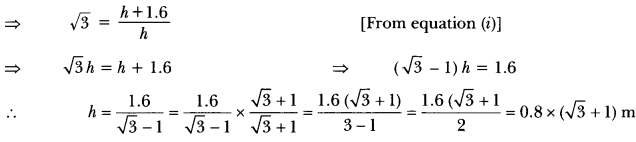
Hence, height of the pedestal is 0.8 (√3 + 1) m.

Question:A 1.2 m tall girl spots a balloon moving with the wind in a horizontal line at a height of 88.2 m from the ground. The angle of elevation of the balloon from the eyes of the girl at any instant is 60°. After some time, the angle of elevation reduces to 30° (Fig. 11.40). Find the distance travelled by the balloon during the interval.

Solution:

Let A and B be two positions of the balloon and G be the point of observation. (eyes of the girl)
Now, we have
AC = BD = BQ – DQ = 88.2 m – 1.2 m = 87 m .
∠AGC = 60°, ∠BGD = 30°
Now, in ∆AGC, we have

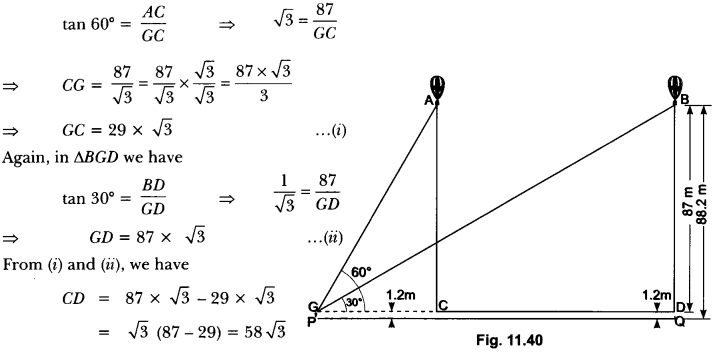
Hence, the balloon travels 58 √3 metres.

Question:A straight highway leads to the foot of a tower. A man standing at the top of the tower observes a car at an angle of depression of 30°, which is approaching the foot of the tower with a uniform speed. Six seconds later, the angle of depression of the car is found to be 60°. Find the time taken by the car to reach the foot of the tower from this point.

Solution:

Let OA be the tower of height h, and P be the initial position of the car when the angle of depression is 30°.
After 6 seconds, the car reaches to such that the angle of depression at Q is 60°. Let the speed of the car be v metre per second. Then,
PQ = 6υ (∵ Distance = speed × time)
and let the car take t seconds to reach the tower OA from Q (Fig. 11.41). Then, OQ = υt metres.
Now, in ∆AQO, we have

Hence, the car will reach the tower from Q in 3 seconds.

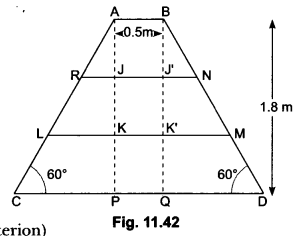
Question:In Fig. 11.42, ABDC is a trapezium in which AB || CD. Line segments RN and LM are drawn parallel to AB such that AJ = JK = KP. If AB = 0.5 m and AP = BQ = 1.8 m, find the lengths of AC, BD, RN and LM.

Solution:

We have,
AP = 1.8 m
AJ = JK = KP = 0.6 m
AK = 2AJ = 1.2 m
In ∆ARJ and ∆BNJ’ we have
AJ = BJ, ∠ARJ = ∠BNJ = 60°
and ∠AJR = ∠BJ’N = 90°
∴ ∆ARJ ≅ ∆BNJ
⇒ RJ = NJ (By AAS congruence criterion)
Similarly, ∆ALK ≅ ∆BMK”
⇒ LK = MK”
In ∆ARJ,

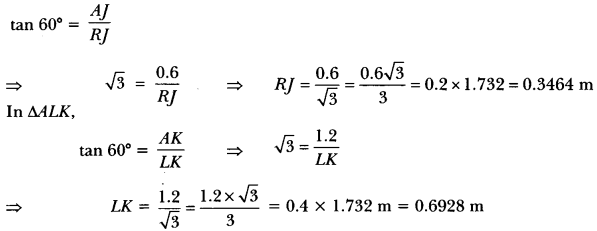
Since ∆ACP ≅ ∆BDQ
So, BD = AC = 2.0784 m
Now, RN = RJ + JJ + J’N
= 2RJ + AB [∵ RJ = J’ N and JJ = AB]
= 2 × 0.3464 +0.5 = 1.1928 m
Length of step LM = LK + KK + KM
= 2LK + AB [∵ LK = K M and KK = AB]
= 2 × 0.6928 + 0.5 = 1.8856 m
Thus, length of each leg = 2.0784 m = 2.1 m
Length of step RN = 1.1928 m = 1.2 m
and, length of step LM = 1.8856 m = 1.9 m

Question:Two poles of equal heights are standing opposite to each other on either side of the road, which is 80 m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60° and 30°, respectively. Find the height of the poles and the distances of the point from the poles.

Solution:

n:

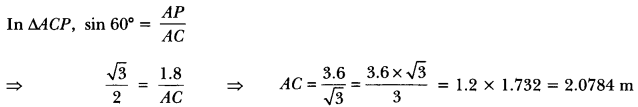
Let AB and CD be two poles of equal height h metre and let P be any point between the poles, such that
∠APB = 60° and ∠DPC = 30°
The distance between two poles is 80m.(Given)
Let AP = x m, then PC = (80 – x) m.
h’m Now, in ∆APB, we have

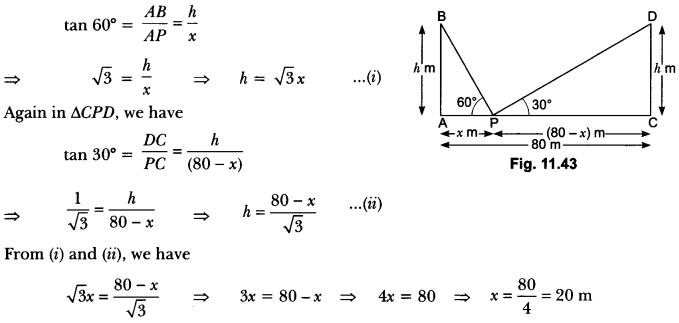
Now, putting the value of x in equation (i), we have
h = √3 × 20 = 20 √3
Hence, the height of the pole is 20 √3 m and the distance of the point from first pole is 20 m and that of the second pole is 60 m.