Case study Questions in Class 9 Mathematics Chapter 1 are very important to solve for your exam. Class 9 Maths Chapter 1 Case Study Questions have been prepared for the latest exam pattern. You can check your knowledge by solving Class 9 Maths Case Study Questions Chapter 1 Real Numbers
Join our Telegram Channel, there you will get various e-books for CBSE 2024 Boards exams for Class 9th, 10th, 11th, and 12th.
In CBSE Class 9 Maths Paper, Students will have to answer some questions based on Assertion and Reason. There will be a few questions based on case studies and passage-based as well. In that, a paragraph will be given, and then the MCQ questions based on it will be asked.
Real Numbers Case Study Questions With Answers
Here, we have provided case-based/passage-based questions for Class 9 Maths Chapter 1 Real Numbers
Case Study/Passage-Based Questions
Case Study 1: A Mathematics Exhibition is being conducted in your school and one of your friends is making a model of a factor tree. He has some difficulty and asks for your help in completing a quiz for the audience.
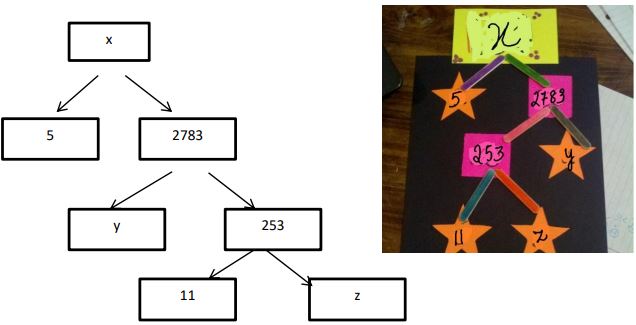
Observe the following factor tree and answer the following:
1. What will be the value of x?
a) 15005
b) 13915
c) 56920
d) 17429
Answer: b) 13915
2. What will be the value of y?
a) 23
b) 22
c) 11
d) 19
Answer: c) 11
3. What will be the value of z?
a) 22
b) 23
c) 17
d) 19
Answer: b) 23
4. According to the Fundamental Theorem of Arithmetic 13915 is a
a) Composite number
b) Prime number
c) Neither prime nor composite
d) Even number
Answer: a) Composite number
5. The prime factorization of 13915 is
a) 5 × 113 × 132
b) 5 × 113 × 232
c) 5 × 112 × 23
d) 5 × 112 × 132
Answer: c) 5 × 112 × 23
Case Study 2: Srikanth has made a project on real numbers, where he finely explained the applicability of exponential laws and divisibility conditions on real numbers. He also included some assessment questions at the end of his project as listed below.
Answer them.
(i) For what value of n, 4n ends in 0?
(a) 10
(b) when n is even
(c) when n is odd
(d) no value of n
Answer: (d) no value of n3
(ii) If a is a positive rational number and n is a positive integer greater than 1, then for what value of n, an is a rational number?
(a) when n is any even integer
(b) when n is any odd integer
(c) for all n > 1
(d) only when n=0
Answer: (c) for all n > 1
(iii) If x and y are two odd positive integers, then which of the following is true?
(a) x2+y2 is even
(b) x2+y2 is not divisible by 4
(c) x2+y2 is odd
(d) both (a) and (b)
Answer: (d) both (a) and (b)
(iv) The statement ‘One of every three consecutive positive integers is divisible by 3’ is
(a) always true
(b) always false
(c) sometimes true
(d) None of these
Answer:(a) always true
(v) If n is any odd integer, then n2 – 1 is divisible by
(a) 22
(b) 55
(c) 88
(d) 8
Answer: (d) 8
Hope the information shed above regarding Case Study and Passage Based Questions for Class 9 Mathematics Chapter 1 Real Numbers with Answers Pdf free download has been useful to an extent. If you have any other queries about CBSE Class 9 Maths Real Numbers Case Study and Passage Based Questions with Answers, feel free to comment below so that we can revert back to us at the earliest possible
By Team Study Rate

