We have provided you with Extra and Important Questions from Class 10 Maths Chapter 12 Areas Related to Circles. This Extra and Important Questions will help you to score 100% in your Board Exams. These extra questions will be helpful to revise the important topics and concepts.

Areas Related to Circles Class 10 Important Questions with Answers Maths Chapter 12

Extra Questions for Class 10 Maths Chapter 12 Very Short Answer Type

Question:

Find the area of a square inscribed in a circle of diameter p cm.

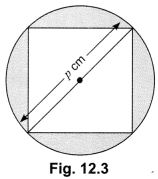
Solution:

Diagonal of the square = p cm
∴ p² = side² + side²
⇒ p² = 2side²
or side² = p²/2 cm² = area of the square

Question:

Find the area of the circle inscribed in a square of side a cm.

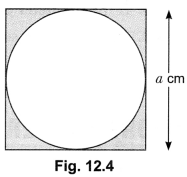
Solution:

Diameter of the circle = a

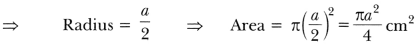
Question:Find the area of a sector of a circle whose radius is and length of the arc is l.

Solution:

Area ola sector ola circle with radius r

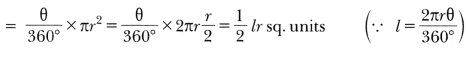
Question:Find the ratio of the areas of a circle and an equilateral triangle whose diameter and a side are respectively equal.

Solution:

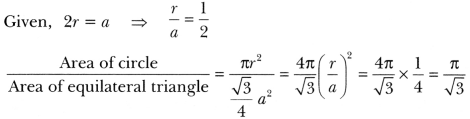
Question:If circumference and the area of a circle are numerically equal, find the diameter of the circle.

Solution:Given, 2πr = πr²
⇒ 2r = r²
⇒ r(r – 2) = 0 or r = 2
i.e. d = 4 units

Question:The radius of a wheel is 0.25 m. Find the number of revolutions it will make to travel a distance of 11 km.

Solution:

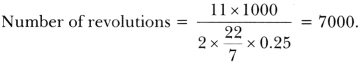
Question:If the diameter of a semicircular protractor is 14 cm, then find its perimeter.

Solution:

Perimeter of a semicircle = πr + 2r
= 22/7 × 7 + 2 × 7 = 22 + 14 = 36cm

Question:

If a square is inscribed in a circle, what is the ratio of the areas of the circle and the square?

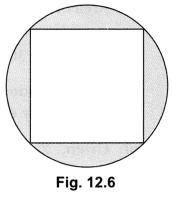
Solution:

Let radius of the circle be r units.
Then, diagonal of the square = 2r

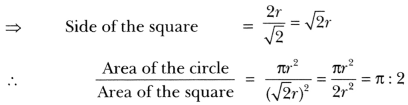
Question:What is the area of the largest triangle that is inscribed in a semi circle of radius r unit?

Solution: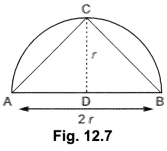

Area of largest ∆ABC = 12 × AB × CD
12 × 2r × r = r² sq. units

Question:What is the angle subtended at the centre of a circle of radius 10 cm by an arc of length 5π cm?

Solution:

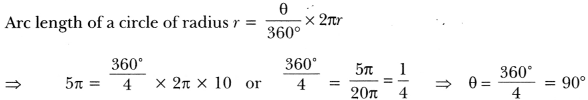
Question:

What is the area of the largest circle that can be drawn inside a 4 rectangle of length a cm and breadth b cm (a > b)?

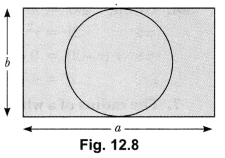
Solution:

Diameter of the largest circle that can be inscribed in the given b
rectangle = b cm
∴ Radius = b/2 cm

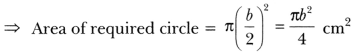
Extra Questions for Class 10 Maths Chapter 12 Short Answer Type

Question:Difference between the circumference and radius of a circle is 37 cm. Find the area of circle.

Solution:

Given 2π r – r = 37
or r (2π – 1) = 37

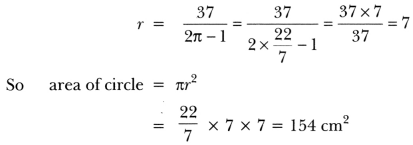
Question:Find the area of a circle whose circumference is 22 cm.

Solution:

Let r be the radius of the circle. Then,
Circumference = 22 cm

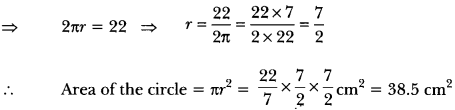
Question:Find the area of a sector of a circle with radius 6 cm if angle of the sector is 60°.

Solution:

We know that

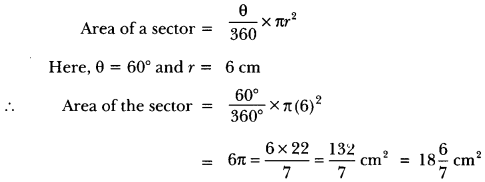
Question:Find the area of a quadrant of a circle whose circumference is 22 cm.

Solution:

Let r be the radius of circle, then circumference = 22 cm

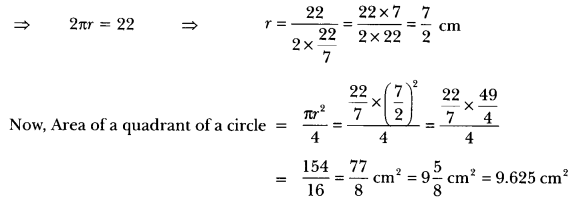
Question:The length of the minute hand of a clock is 14 cm. Find the area swept by the minute hand in 5 minutes.

Solution:

Since the minute hand rotates through 6° in one minute, therefore, area swept by the minute hand in one minute is the area of a sector of angle 6° in a circle of radius 14 cm.

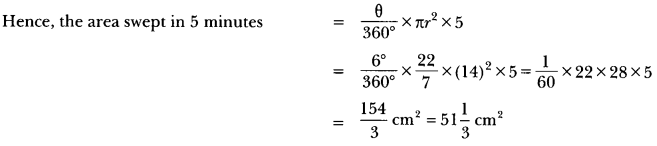
Question:To warn ships for underwater rocks, a lighthouse spreads a red coloured light over a sector of angle 80° to a distance of 16.5 km. Find the area of the sea over which the ships are warned. (Use π = 3.14)

Solution:

We have, r = 16.5 km and 0 = 80°
∴ Area of the sea over which the ships are warned =

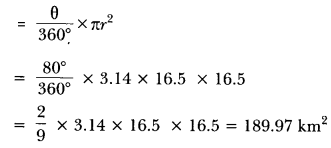
Question:If the perimeter of a semicircular protractor is 66 cm, find the diameter of the protractor

Solution:

Let the radius of the protractor be r сm. Then,
Perimeter = 66 cm
= πr + 2r = 66 [∴ Perimeter of a semicircle = πr + 2r]

Question:A race track is in the form of a ring whose inner circumference is 352 m, and the outer circumference is 396 m. Find the width of the track.

Solution:

Let the outer and inner radii of the ring be R m and r m respectively. Then,
2πR = 396 and 2πr = 352

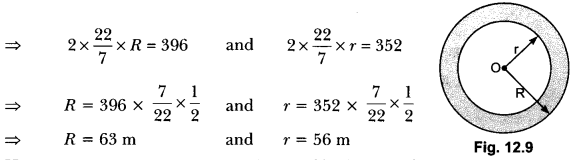
Hence, width of the track = (R – r) m = (63 – 56) m = 7 m

Question:Figure 12.37 depicts an archery target marked with its five scoring areas from the centre outwards as Gold, Red, Blue, Black and White. The diameter of the region representing Gold score is 21 cm and each of the other bands is 10.5 cm wide. Find the area of each of the five scoring regions.

Solution:

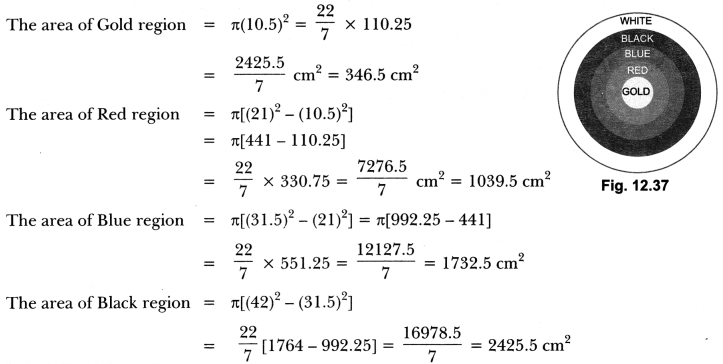
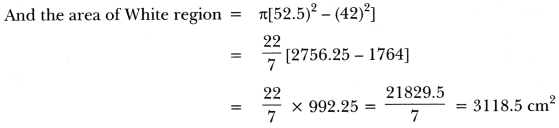
Question:The short and long hands of a clock are 4 cm and 6 cm long respectively. Find the sum of distances travelled by their tips in 2 days.

Solution:

In 2 days, the short hand will complete 4 rounds.
Distance moved by its tip = 4 (Circumference of a circle of radius 4 cm)

Extra Questions for Class 10 Maths Chapter 12 Long Answer Type

Question:Fig. 12.38, depicts a racing track whose left and right ends are semicircular. The distance between the two inner parallel line segments is 60 m and they are each 106 m long. If the track is 10 m wide, find:
(i) the distance around the track along its inner edge.
(ii) the area of the track.

Solution:

n: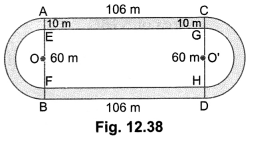

Here, we have
OE = O’G = 30 m
AE = CG = 10 m
OA = O’C = (30 + 10) m = 40 m
AC = EG = FH = BD = 106 m

(i) The distance around the track along its inner edge
= EG + FH + 2 × (circumference of the semicircle of radius OE = 30cm)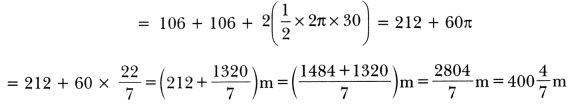

(ii) Area of the track = Area of the shaded region
= Area of rectangle AEGC + Area of rectangle BFHD + 2 (Area of the semicircle of radius 40 m – Area of the semicircle with radius 30 m)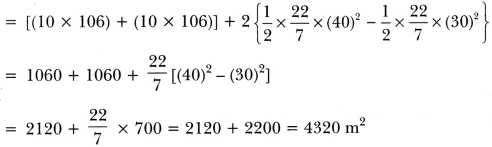

Question:The area of an equilateral triangle ABC is 17320.5 cm. With each vertex of the triangle as centre, a circle is drawn with radius equal to half the length of the side of the triangle (see Fig. 12.39). Find the area of the shaded region. (Use π = 3.14 and √3 = 1.73205)

Solution:

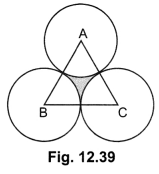
Let each side of the equilateral triangle be x cm. Then,
Area of equilateral triangle ABC = 17320.5 cm (Given)

Question:In a circular table cover of radius 32 cm, a design is formed leaving an equilateral triangle ABC in the middle as shown in Fig. 12.40. Find the area of the design.

Solution:

Here, ∆ABC is an equilateral triangle. Let O be the circumcentre of circumcircle.
Radius, r = 32 cm.
Now, area of circle = πr²

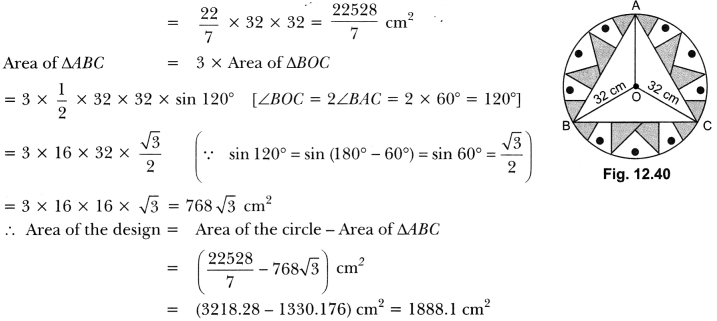
Question:In Fig. 12.41, AB and CD are two diameters of a circle (with centre O) perpendicular to each other and OD is the diameter of the smaller circle. If OA = 7 cm, find the area of the shaded region.

Solution:

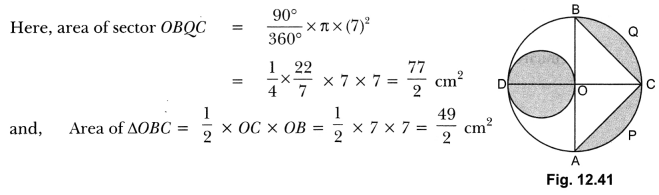
Question:In Fig. 12.42 ABC is a quadrant of a circle of radius 14 cm and a semicircle is drawn with BC as diameter. Find the area of the shaded region.

Solution:

In ∆ABC, we have

Hence, area of the shaded region = Area of the semi-circle BQC – Area of the segment BPC
= (154 – 56)cm² = 98cm²

Question:

In Fig 12.43, a circle is inscribed in an equilateral triangle ABC of side 12 cm. Find the radius of inscribed circle and the area of the shaded region. [Use π = 3.14 and √3 = 1.73]

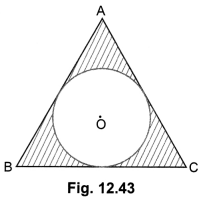
Solution:

Construction:
Join OA, OB and OC
Draw OZ ⊥ BC, OX ⊥ AB and OY ⊥ AC.
Let the radius of the circle be r сm.
Area of ∆ABC = Area of ∆AOB + Area of ∆BOC + Area of ∆AOC

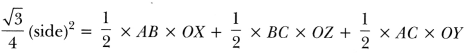
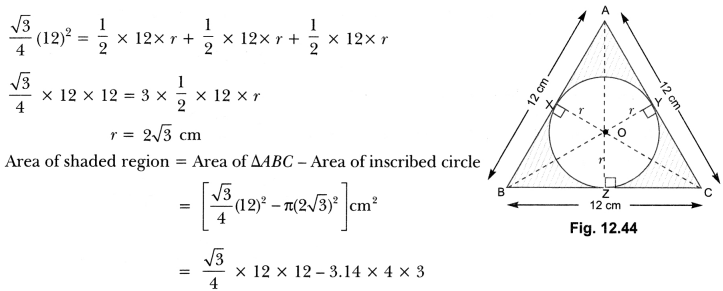
= 1.73 × 3 × 12 – 3.14 × 4 × 3
= 62.28 – 37.68 = 24.6 cm