We have provided you with Extra and Important Questions from Class 10 Maths Chapter 2 Polynomials. This Extra and Important Questions will help you to score 100% in your Board Exams. These extra questions will be helpful to revise the important topics and concepts.

Polynomials Class 10 Important Questions with Answers Maths Chapter 2

Extra Questions for Class 10 Maths Chapter 2 Very Short Answer Type

Question: If on division of a polynomial p(x) by a polynomial g(x), the quotient is zero, what is the relation between the degrees of p(x) and g(x)?

Answer: Since the quotient is zero, therefore , deg p(x) < deg g(x)

Question: Can x – 2 be the remainder on division of a polynomial p(x) by x + 3?

Answer: No, as degree (x – 2) = degree (x + 3)

Question: Find the quadratic polynomial whose zeros are -3 and 4.[NCERT Exemplar]

Answer: Sum of zeros = -3 + 4 = 1,
Product of zeros = – 3 x 4 = -12
∴ Required polynomial = x² – x – 12

Question: If one zero of the quadratic polynomial x² – 5x – 6 is 6 then find the other zero.

Answer: Let α,6 be the zeros of given polynomial.
Then α + 6 = 5 ⇒ α = -1

Question: If both the zeros of the quadratic polynomial ax² + bx + c are equal and opposite in sign, then find the value of b.

Answer: Let α and -α be the roots of given polynomial.
Then α + (-α) = 0 ⇒ −ba=0 ⇒ b = 0.

Question: What number should be added to the polynomial x² – 5x + 4, so that 3 is the zero of the polynomial?

Answer: Let f(x) = x² – 5x + 4
Then f(3) = 3² – 5 x 3 + 4 = -2
For f(3) = 0, 2 must be added to f(x).

Question: Can a quadratic polynomial x² + kx + k have equal zeros for some odd integer k > 1?

Answer: No, for equal zeros, k = 0,4 ⇒ k should be even.

Question: If the zeros of a quadratic polynomial ax² + bx + c are both negative, then can we say a, b and c all have the same sign? Justify your answer.

Answer: Yes, because −ba = sum of zeros < 0, so that ba=0 > 0. Also the product of the zeros = ca=0 > 0.

Question: If the graph of a polynomial intersects the x-axis at only one point, can it be a quadratic polynomial?

Answer: Yes, because every quadratic polynomial has at the most two zeros.

Question: If the graph of a polynomial intersects the x-axis at exactly two points, is it necessarily a quadratic polynomial?

Answer: No, x⁴ – 1 is a polynomial intersecting the x-axis at exactly two points.

Extra Questions for Class 10 Maths Chapter 2 Short Answer Type

Question: If one of the zeros of the quadratic polynomial f(x) = 4x² – 8kx – 9 is equal in magnitude but opposite in sign of the other, find the value of k.

Answer: Let one root of the given polynomial be α.
Then the other root = -α
Sum of the roots = (-α) + α = 0
⇒ −b/a = 0 or −8k/4 = 0 or k = 0

Question: Find a quadratic polynomial each with the given numbers as the sum and product of its zeros respectively.

Answer: Let α, β be the zeros of polynomial.

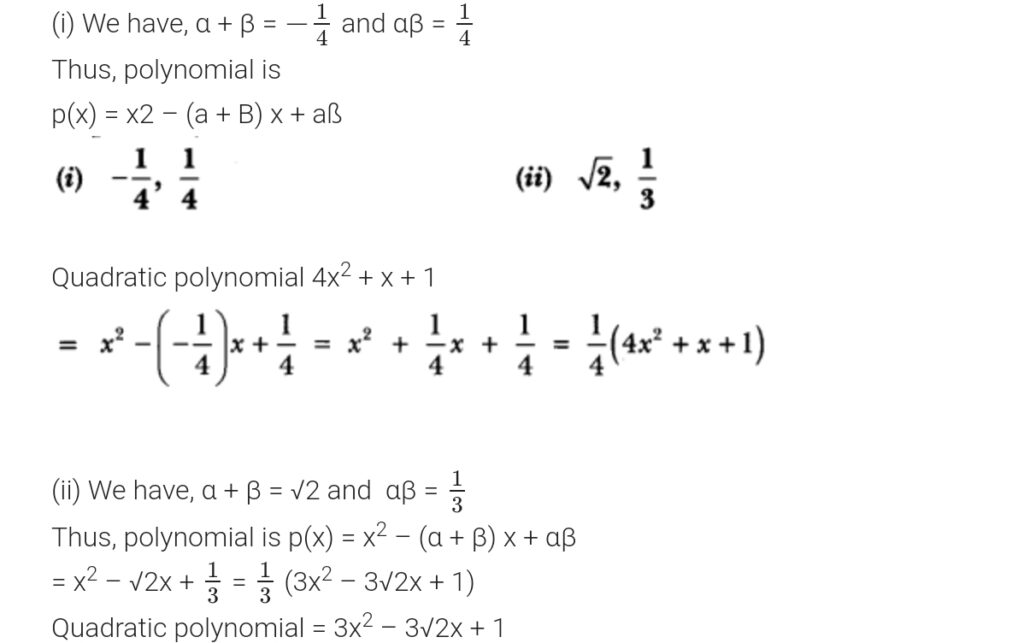
Question: If the product of two zeros of the polynomial p(x) = 2x³ + 6x² – 4x + 9 is 3, then find its third zero.

Answer: Let α, β, γ be the roots of the given polynomial and αβ = 3
Then αβγ = −9/2
⇒ 3 x γ = −9/2 or γ = −3/2

Question: Given that one of the zeros of the cubic polynomial ax³ + bx² + cx + d is zero, find the product of the other two zeros.

Answer: Let α, β, γ be the roots of the given polynomial and α = 0.
Then αβ + βγ + γα = c/a ⇒ βγ = c/a

Question: If one root of the polynomial p(y) = 5y² + 13y + m is reciprocal of other, then find the value of m.

Answer:

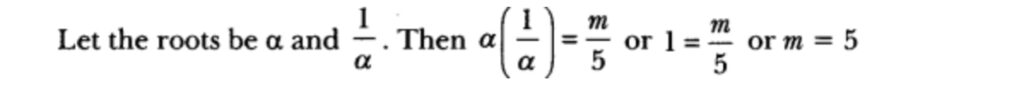
Question: If the polynomial (x⁴ + 2x³ + 8x² + 12x + 18) is divided by another polynomial (x² + 5), the remainder comes out to be (px +q). Find values of p and q.

Answer: Let f(x) = (x⁴ + 2x³ + 8x² + 12x + 18) and g(x) = (x² + 5)
On dividing f(x) by g(x), we get

Now, px + 9 = 2x + 3 ⇒ p = 2,q = 3 (By comparing the coefficient of x and constant term).

Question: If one zero of the polynomial 2x² + 3x + λ is 1/2 find the value of and other zero.

Answer: Let P(x) = 2x² + 3x + λ

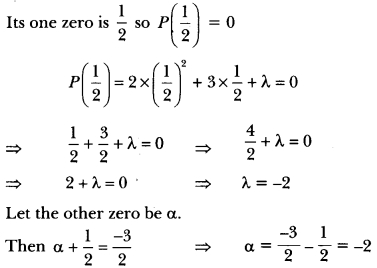
Question: If one zero of the polynomial 3x² – 8x + 2k + 1 is seven times the other, find the value of k.

Answer: Let α and β be the zeros of the polynomial. Then as per question β = 7α

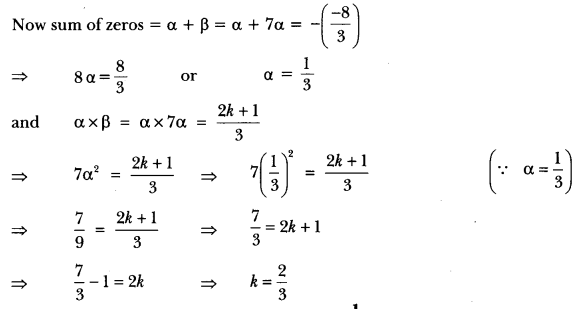
Question: If α and β are the zeros of the polynomial 6y² – 7y + 2, find a quadratic polynomial whose zeros are 1α and 1β.

Answer: Let p(y) = 6y² – 7y + 2

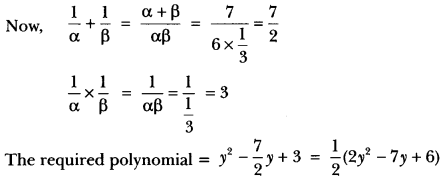
Question: Obtain the zeros of quadratic polynomial 3x² – 8x + 4√3 and verify the relation between its zeros and coefficients.

Answer:We have,

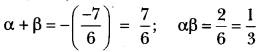
Question: What must be added to f(x) = 4x⁴ + 2x³ – 2x² + x – 1 so that the resulting polynomial is divisible
by g(x) = x² + 2x – 3?

Answer:
By division algorithm, we have
f(x) = g(x) × q(x) + r(x)
= f(x) – r(x) = g(x) × q(x) ⇒ f(x) + {-r(x)} = g(x) × q(x)
Clearly, RHS is divisible by g(x). Therefore, LHS is also divisible by g(x). Thus, if we add –r(x) to f(x), then the resulting polynomial is divisible by g(x). Let us now find the remainder when f(x) is divided by g(x).

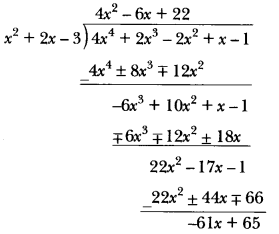
∴ r(x) = -61x + 65 or -r(x) = 61x – 65
Hence, we should add –r(x) = 61x – 65 to f(x) so that the resulting polynomial is divisible by g(x).

Extra Questions for Class 10 Maths Chapter 2 Long Answer Type

Question: Given that √2 is a zero of the cubic polynomial 6x³ + √2x² – 10x – 4√2, find its other zeros.

Solution:
The given polynomial is f(x) = (6x³ +√2x² – 10x – 4√2). Since √2 is the zero of f(x), it follows that (x – √2) is a factor of f(x).
On dividing f(x) by (x – √2), we get

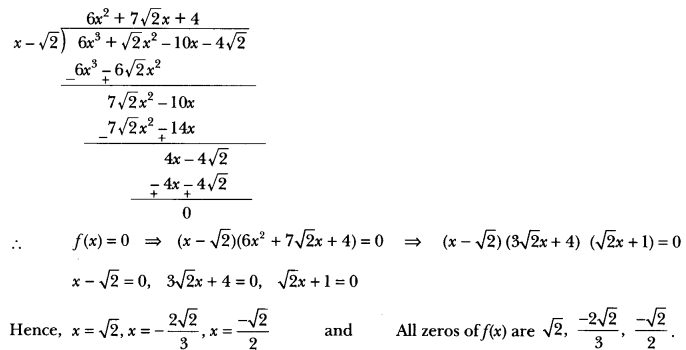
Question: Obtain all other zeros of 3x⁴ + 6x³ – 2x² – 10x – 5, if two of its zeros are √5/3 and -√5/3.

Solution:

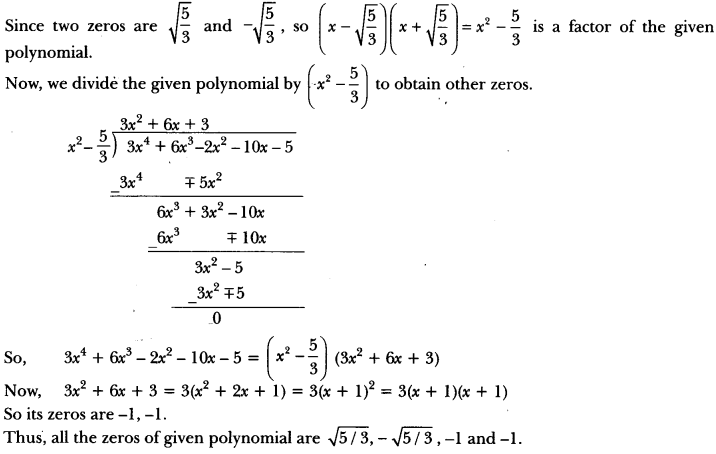
Question: If the remainder on division of x³ – kx² + 13x – 21 by 2x – 1 is -21, find the quotient and the value of k. Hence, find the zeros of the cubic poIynomia1 x³ – kx² + 13x.

Solution:
Let f(x) = x³ – kx² + 13x – 21

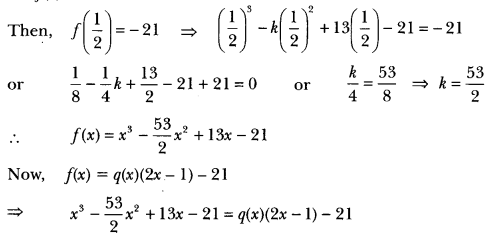
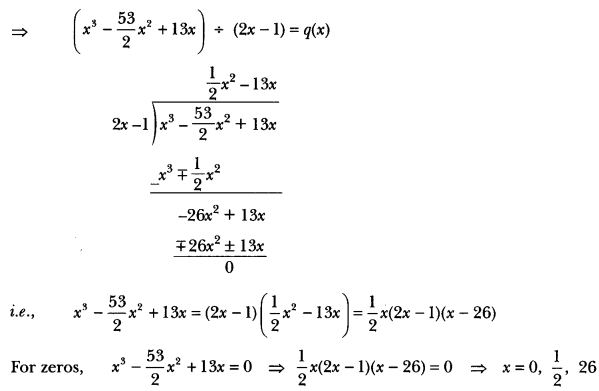
Question: Find the zeros of the polynomial f(x) = x³ – 5x² – 2x + 24, if it is given that the product of its two zeros is 12.

Solution:
Let α, β and γ be the zeros of polynomial (fx) such that αβ = 12.

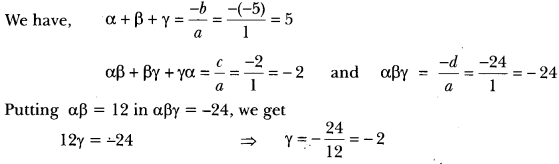
Now, α + β + γ = 5 α + β – 2 = 5
= α + β = 7 a = 7 – β
= (7 – β) β =12 ⇒ 7β – β² – 12
= β² + 7β + 12 = 0 ⇒ β² – 3β – 4β + 12 = O
= β = 4 or β = 3
β = 4 or β = 3
∴ α = 3 or α = 4

Question: Find a cubic polynomial with the sum of the zeros, sum of the products of its zeros taken two at a time, and the product of its zeros as 2, -7, -14 respectively.

Solution:
Let the cubic polynomial be p(x) = ax³ + bx² + cx + d. Then

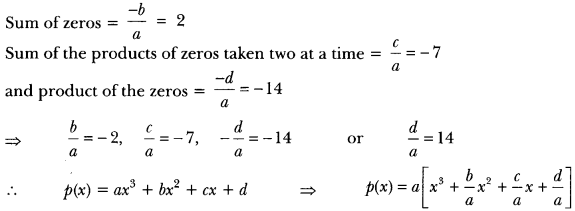
p(x) = a[x³ + (-2)x² + (-7)x + 14] ⇒ p(x) = a[x3 – 2x² – 7x + 14]
For real value of a = 1, p(x) = x³ – 2x² – 7x + 14

Question: Verify that the numbers given alongside the cubic polynomial below are their zeros. Also verify the relationship between the zeros and the coefficients.
x³ – 4x² + 5x – 2; 2,1,1

Solution:
Let p(x) = x³ – 4 x² + 5x – 2
On comparing with general polynomial px) ax³ + bx² + cx + d, we get a = 1, b = -4, c = 5 and d = -2
Given zeros 2, 1, 1.
∴ p(2) = (2)³ – 4(2)² + 5(2) – 2 = 8 – 16 + 10 – 2 = 0
and p(1) = (1)³ – 4(1)² + 5(1) – 2 = 1 – 4 + 5 – 2 = 0
Hence, 2, 1 and I are the zeros of the given cubic polynomial.
Again, consider α = 2, β = 1, γ = 1
∴ α + 13 + y = 2 + 1 + 1 = 4

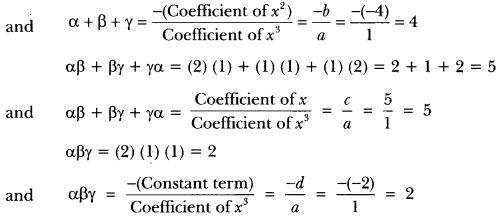
Question: If the polynomial f(x) = x⁴ – 6x³ + 16x² – 25x + 10 is divided by another polynomial x² – 2x + k, the remainder comes out to be x + a. Find k and a.

Solution:
By division algorithm, we have Dividend = Divisor × Quotient + Remainder
⇒ Dividend – Remainder = Divisor × Quotient
⇒ Dividend – Remainder is always divisible by the divisor.
When f(x) = – 6x³ + 16x² – 25x + 10 is divided by x² – 2x + k the remainder comes out to be x + a.
∴ f(x) – (x + a) = x⁴ – 6x³+ 16x² – 25x + 10 – (x + a)
= x⁴ – 6x³ + 16x² – 25x + 10 – x – a x⁴ – 6x³ + 16x² – 26x + 10 – a
is exactly divisible by x² – 2x + k
Let us now divide x⁴ – 6x³ + 16x² – 26x + 10 – a by x² – 2x + k.

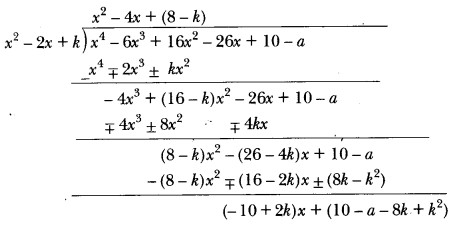
For f(x) – (x + a) = x⁴ – 6x³ + 16x² – 26x + 10 – a to be exactly divisible by x² – 2x + k, we must
have (-10 + 2k)x + (10 – a – 8k + k²) = 0 for all x
= – 10 + 2k = 0 and 10 – a – 8k + k² = 0
⇒ k = 5 and 10 – a – 40 + 25 = 0
⇒ k = 5 and a – 5