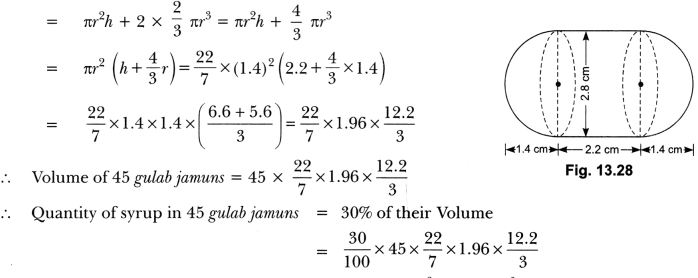We have provided you with Extra and Important Questions from Class 10 Maths Chapter 13 Surface Areas and Volumes. This Extra and Important Questions will help you to score 100% in your Board Exams. These extra questions will be helpful to revise the important topics and concepts.

Surface Areas and Volumes Class 10 Important Questions with Answers Maths Chapter 13

Extra Questions for Class 10 Maths Chapter 13 Very Short Answer Type

Question: What is the capacity of a cylindrical vessel with a hemispherical portion raised upward at the bottom?.

Solution:

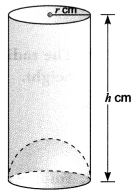
Capacity of the given vessel
= capacity of cylinder – capacity of hemisphere

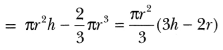
Question: 

A solid cone of radius r and height h is placed over a solid cylinder having same base radius and height as that of a cone. What is the total surface area of the combined solid?

Solution:
The total surface area of the combined solid in Fig.
= curved surface area of cone + curved surface area of cylinder + area of the base.

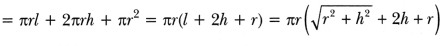
Question: Two identical solid hemispheres of equal base radius r сm are struck together along their bases. What will be the total surface area of the combination?

Solution:

The resultant solid will be a sphere of radius r whose total surface area is 4πr².

Question: A solid ball is exactly fitted inside the cubical box of side a. What is the volume of the ball?

Solution:

Diameter of the solid ball = edge of the cube = a

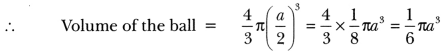
Question: If two cubes of edge 5 cm each are joined end to end, find the surface area of the resulting cuboid.

Solution:Total length (l) = 5 + 5 = 10 cm
Breadth (b) = 5 cm, Height (h) = 5 cm
Surface Area = 2 (lb + bh + lh)
= 2(10 × 5 + 5 × 5 + 5 × 10) = 2 × 125 = 250 cm²

Question: The radii of the ends of a frustum of a cone 40 cm high are 20 cm and 11 cm. Find its slant height.

Solution:

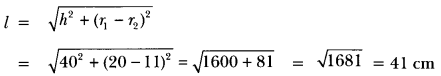
Question: A cone, a hemisphere and a cylinder stand on equal bases and have the same height. What is the ratio of their volumes?

Solution:

Volume of a cone: Volume of a hemisphere: Volume of a cylinder

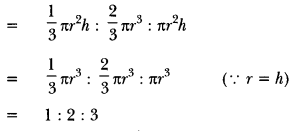
Question: What is the ratio of the volume of a cube to that of a sphere which will fit inside it?

Solution:

Let edge of the cube be ‘a’.
Then, diameter of the sphere that will fit inside the given cube = a
∴ Volume of the cube : Volume of the sphere

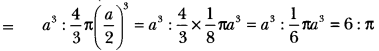
Question: The slant height of the frustum of a cone is 5 cm. If the difference between the radii of its two circular ends is 4 cm, find the height of the frustum.

Solution:Let r and R be radii of the circular ends of the frustum of the cone.
Then, R – r = 4, l = 5
We know, l² = (R – r)² + h²
⇒ 5² = 4² + h² or h² = 25 – 16 = 9
⇒ h = 3 cm

Question: If the slant height of the frustum of a cone is 10 cm and the perimeters of its circular base are 18 cm and 28 cm respectively. What is the curved surface area of the frustum?

Solution:

Let r and R be the radii of the two circular ends of the frustum of the cone.
Then, 2πr = 18 and 2πR = 28

Question: A solid is in the shape of a cone standing on a hemisphere with both their radii being equal to 1 cm and the height of the cone is equal to its radius. Find the volume of the solid in terms of T.

Solution:

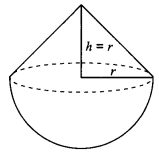
We have,
Height
of cone is equal to its radius
i.e., h =r = 1 cm (Given)
Also, radius of hemisphere = r = 1 cm
Now, Volume of the solid
= Volume of the cone + Volume of the hemisphere

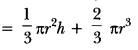
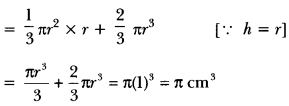
Question: Two cubes each of volume 64 cm³ are joined end to end. Find the surface area of the resulting cuboid.

Solution:

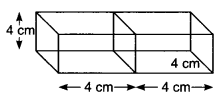
Let the length of each edge of the cube of volume 64 cm³ be x cm.
Then, Volume = 64 cm³
⇒ x² = 64
⇒ x² = 4³
⇒ x = 4 cm
4 cm The dimensions of cuboid so formed are
l = Length = (4 + 4) cm = 8 cm
b = Breadth = 4 cm and h = Height = 4 cm
∴ Surface area of the cuboid = 2 (lb + bh + lh)
= 2 (8 × 4 + 4 × 4 + 8 × 4)
= 2 (32 + 16 + 32)
= 160 cm²

Question: A cubical block of side 7 cm is surmounted by a hemisphere. What is the greatest diameter the hemisphere can have? Find the surface area of the solid.

Solution:

The greatest diameter that a hemisphere can have = 7 cm = l
Radius of the hemisphere (R) = \(\frac{7}{2}\) cm
∴ Surface area of the solid after surmounting hemisphere
= 6l² – πR² + 2πR² = 6l² + πR²

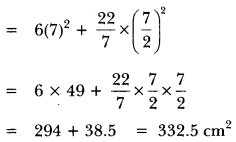
Question: The dimensions of a solid iron cuboid are 4.4 m × 2.6 m × 1.0 m. It is melted and recast into a hollow cylindrical pipe of 30 cm inner radius and thickness 5 cm. Find the length of the pipe.

Solution:

Let the length of pipe by h m.
Volume of cuboid = 4.4 × 2.6 × 1 m²
Inner and outer radii of cylindrical pipe are 30 cm, (30 + 5) cm = 35 cm

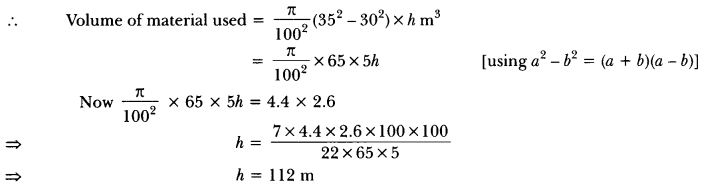
Question: A toy is in the form of a cone of radius 3.5 cm mounted on a hemisphere of same radius. The total height of the toy is 15.5 cm. Find the total surface area of the toy.
OR
A toy is in the form of a cone of radius 3.5 cm mounted on a hemisphere of same radius on its circular face. The total height of the toy is 15.5 cm. Find the total surface area of the toy.

Solution:

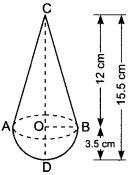
We have,
CD = 15.5 cm and OB = OD = 3.5 cm
Let r be the radius of the base of cone and h be the height of conical part of the toy.
Then, r = OB = 3.5 cm
h = OC = CD – OD = (15.5 – 3.5) cm = 12 cm

Question: 

A medicine capsule is in the shape of a cylinder with two hemispheres stuck to each of its ends (Fig). The length of the entire capsule is 14 mm and the diameter of the capsule is 5 mm. Find its surface area.

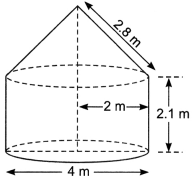
Solution:

Let the radius and height of the cylinder be r сm and h cm respectively. Then,

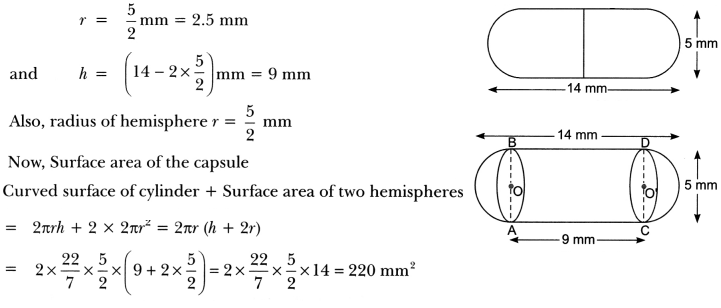
Question: A metallic sphere of radius 4.2 cm is melted and recast into the shape of a cylinder of radius 6 cm. Find the height of the cylinder.

Solution:

We have,
Radius of sphere (r₁) = 4.2 cm, Radius of cylinder (r₂) = 6 cm
Let h cm be the height of cylinder.
Now, since sphere is melted and recast into cylinder
∴ Volume of sphere = Volume of cylinder

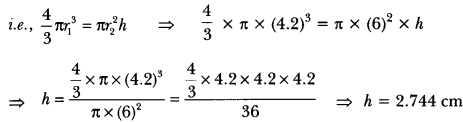
Hence, height of the cylinder is 2.744 cm.

Question: Metallic spheres of radii 6 cm, 8 cm and 10 cm, respectively, are melted to form a single solid sphere. Find the radius of the resulting sphere.

Solution:

Let r be the radius of resulting sphere.
We have,
Volume of resulting sphere = Sum of the volumes of three given spheres

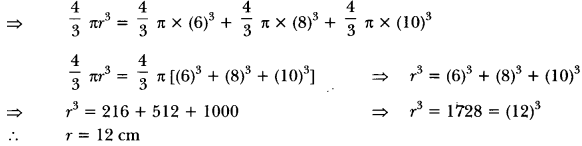
Hence, the radius of the resulting sphere is 12 cm.

Question: How many silver coins, 1.75 cm in diameter and of thickness 2 mm, must be melted to form a cuboid of dimensions 5.5 cm × 10 cm × 3.5 cm?

Solution:

We have,

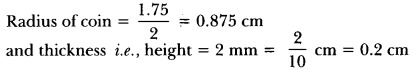
Question: A drinking glass is in the shape of a frustum of a cone of height 14 cm. The diameters of its two circular, ends are 4 cm and 2 cm. Find the capacity of the glass.

Solution:

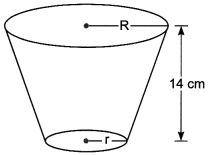
We have, R = 2 cm, r = 1 cm, h = 14 cm
∴ Capacity of the glass = Volume of the frustum

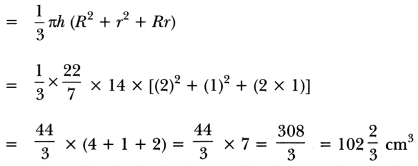
Question: 

Two spheres of same metal weigh 1 kg and 7 kg. The radius of the smaller sphere is 3 cm. The two spheres are melted to form a single big sphere. Find the diameter of the new sphere.

Solution:

∴ Diameter of new sphere = 12 cm.

Question: A hemispherical bowl of internal diameter 36 cm contains liquid. This liquid is filled into 72 cylindrical bottles of diameter 6 cm. Find the height of the each bottle, if 10% liquid is wasted in this transfer.

Solution:

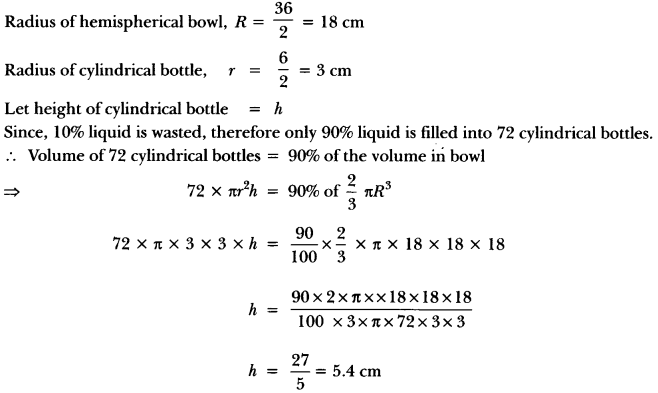
Question: A cylindrical tub, whose diameter is 12 cm and height 15 cm is full of ice cream. The whole ice cream is to be divided into 10 children in equal ice-cream cones, with conical base surmounted by hemispherical top. If the height of conical portion is twice the diameter of base, find the diameter of conical part of ice-cream cone.

Solution:

Volume of ice-cream in the cylinder = πr²h = (π(6)² × 15) cm³

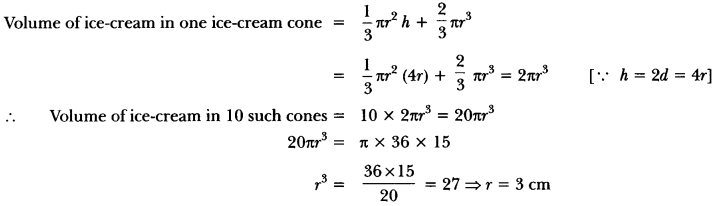
Diameter of conical ice-cream cup = 6 cm

Question: A sphere of diameter 12 cm, is dropped in a right circular cylindrical vessel, partly filled with water. If the sphere is completely submerged in water, the water level in the cylindrical vessel rises by 3\(\frac{3}{9}\) cm. Find the diameter of the cylindrical vessel.

Solution:

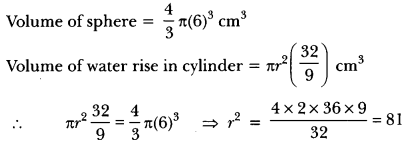
Question: 

From a solid cylinder whose height is 2.4 cm and diameter 1.4 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid to the nearest cm?
OR
From a solid right circular cylinder of height 2.4 cm and radius 0:7 cm, a right circular cone of same height and same radius is cut out. Find the total surface area of the remaining solid.

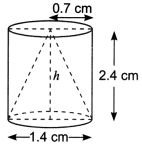
Solution:

We have,
0.7 cm Radius of the cylinder = 1.4/2 = 0.7 cm
Height of the cylinder = 2.4 cm
Also, radius of the cone = 0.7 cm
and height of the cone = 2.4 cm

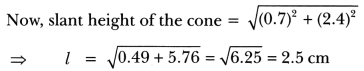
∴ Total surface area of the remaining solid
= Curved surface area of cylinder + Curved surface area of the cone + Area of upper circular base of cylinder
= 2πrh + πrl + πr² = πr(2h + l + r)
= \(\frac{22}{7}\) × 0.7 × [2 × 2.4 + 2.5 + 0.7]
= 22 × 0.1 × (4.8 + 2.5 + 0.7)
= 2.2 × 8.0 = 17.6 cm² = 18 cm²

Question: The decorative block shown in figure is made of two solids a cube and a hemisphere. The base of the block is a cube with edge 5 cm, and the hemisphere fixed on the top has a diameter of 4.2 cm. Find the total surface area of the block. (Use π = \(\frac{22}{7}\))

Solution:

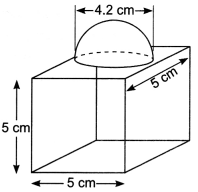
The total surface area of the cube = 6 × (edge)²
= 6 × 5 × 5 cm² = 150 cm
∴ Total surface area of the block
= Total surface area of cube – Base area of hemisphere + Curved surface area of hemisphere
= 150 – πr² + 2πr² = (150 + πr²) cm²

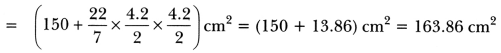
cm² = (150 + 13.86) cm² = 163.86 cm

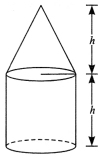
Question: 

Rasheed got a playing top (lattu) as his birthday present, which surprisingly had no colour on it. He wanted to colour it with his crayons. The top is shaped like a cone surmounted by a hemisphere (Fig). The entire top is 5 cm in height and the diameter of the top is 3.5 cm. Find the area he has to colour. (Take π = \(\frac{22}{7}\)

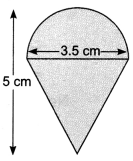
Solution:

Total surface area of the top
= Curved surface area of hemisphere + Curved surface area of cone. Now, the curved surface area of hemisphere = 2πr²

Question: 

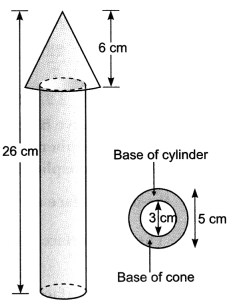
A wooden toy rocket is in the shape of a cone mounted on a cylinder, in Fig. The height of the entire rocket is 26 cm, 6 cm while the height of the conical part is 6 cm. The base of the conical portion has a diameter of 5 cm, while the base diameter of the cylindrical portion is 3 cm. If the conical portion is to be painted orange and the cylindrical portion yellow, find the area of the rocket painted with each of these colours. (Take π = 3.14) 26 cm

Solution:

Denote radius, slant height and height of cone by r, l and h, respectively, and radius and height of cylinder by r’ and h’, respectively. Then r = 2.5 cm, h = 6 cm, r’ = 1.5 cm,
h’ = 26 – 6 = 20 and

Here, the conical portion has its circular base resting on the base of the cylinder, but the base of the cone is larger than the base of the cylinder. So, a part of the base of the cone (a ring) is to be painted. So, the area to be painted orange
= Curved surface area of the cone + Base area of the cone – Base area of the cylinder
= πrl + πr² – π(r’)²
= [(2.5 × 6.5) + (2.5)² – (1.5)²] cm²
= π[20.25] cm²
= 3.14 × 20.25 cm² = 63.585 cm²
Now, the area to be painted yellow
= Curved surface area of the cylinder + Area of one base of the cylinder
= 2πr’h’ + π(r’)² = πr’ (2h’ + r’)
= (3.14 × 1.5) (2 × 20 + 1.5) cm² = 4.71 × 41.5 cm² = 195.465 cm²

Question: Rachel, an engineering student, was asked to make a model shaped like a cylinder with two cones attached at its two ends by using a thin aluminium sheet. The diameter of the model is 3 cm and its length is 12 cm. If each cone has a height of 2 cm, find the volume of air contained in the model that Rachel made. (Assume the outer and inner dimensions of the model to be nearly the same.)

Solution:

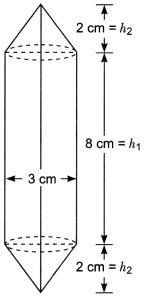
Here, radius of cylindrical portion = \(\frac{3}{2}\)
Height of each cone = 2 cm
Height of cylindrical portion = 12 – 2 – 2 = 8 cm
Volume of the air contained in the model
= Volume of the cylindrical portion of the model + Volume of two conical K ends.

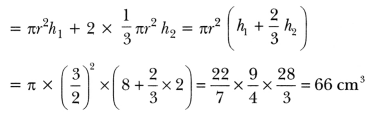
Question: 

A gulab jamun, contains sugar syrup about 30% of its volume. Find approximately how much syrup would be found in 45 gulab jamuns, each shaped like a cylinder with two hemispherical ends with length 5 cm and diameter 2.8 cm (Fig).

Solution:

We have,
Radius of cylindrical portion and hemispherical portion of a gulab jamun
2.8/2 = 1.4 cm
Length of cylindrical portion = 5 – 1.4 – 1.4 = 2.2 cm
Volume of one gulab jamun
= Volume of the cylindrical portion + Volume of the hemispherical ends