We have provided you with Extra and Important Questions from Class 10 Maths Chapter 14 Statistics Class 10 Extra Questions Very Short Answer Type. This Extra and Important Questions will help you to score 100% in your Board Exams. These extra questions will be helpful to revise the important topics and concepts.

Statistics Class 10 Important Questions with Answers Maths Chapter 14

Extra Questions for Class 10 Maths Chapter 14 Very Short Answer Type

Question:Find the class mark of the class 10 – 25.

Solution:

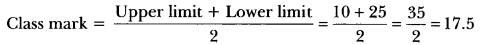
Question:Find the mean of the first five natural numbers.

Solution:

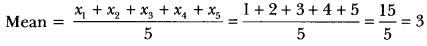
Question:A data has 13 observations arranged in descending order. Which observation represents the median of data?

Solution:

Total no. of observations = 13, which is odd

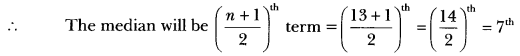
i.e., 7^th term will be the median.

Question:In an arranged señes of an even number of 2n terms which term is median?

Solution:

No. of terms = 2n which are even

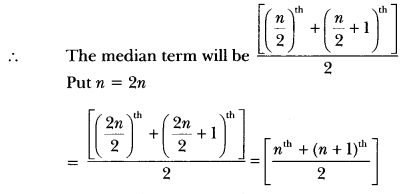
i.e., the mean of n^th and (n + 1)^th term will be the median.

Question:What does the abscissa of the point of intersection of the less than type and of the more than type cumulative frequency curves of a grouped data represent?

Solution:

The abscissa of the point of intersection of the less than type and of the more than type cumulative frequency curves of a grouped data gives its median.

Question:Name the graphical representation from which the mode of a frequency distribution is obtained.

Solution:

The mode of frequency distribution is determined graphically from Histogram.

Question:

Write the modal class for the following frequency distribution:

Solution:Maximum frequency, i.e., 65 corresponds to the class 30 – 40
∴ Modal class is 30 – 40.

Question:

Find the median class of the following distribution:

Solution:

First we find the cumulative frequency

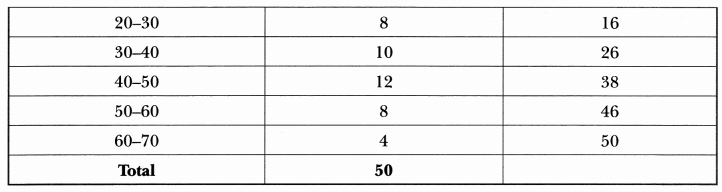
Here, n/2 = 50/2
∴ Median class = 30 – 40.

Question:Find the class marks of classes 15.5 – 18.5 and 50 – 75.

Solution:

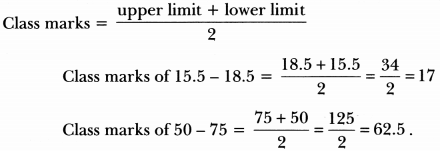
Extra Questions for Class 10 Maths Chapter 14 Short Answer Type

Question:

If the mean of the following distribution is 6, find the value of p.

Solution:

Calculation of mean

Question:

Find the mean of the following distribution:

Solution:

Calculation of arithmetic mean

Question:

The following data gives the information on the observed lifetimes (in hours) of 225 electrical components:

Determine the modal lifetimes of the components.

Solution:

Here, the maximum class frequency is 61 and the class corresponding to this frequency is 60 – 80.
So, the modal class is 60 – 80.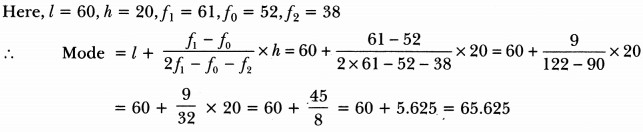

Hence, modal lifetime of the components is 65.625 hours.

Question:

The distribution below gives the weights of 30 students of a class. Find the median weight of the students.

Solution:

Calculation of median

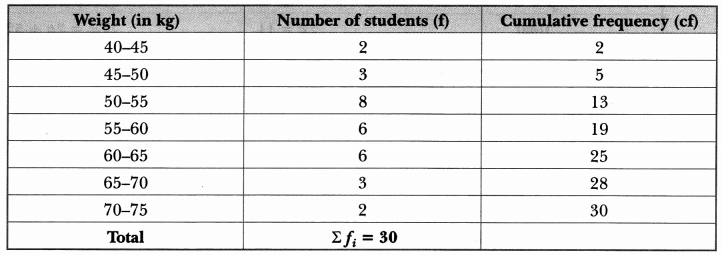
The cumulative frequency just greater than n/2 = 15 is 19, and the corresponding class is 55 – 60.
∴ 55 – 60 is the median class.

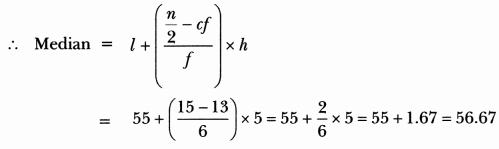
Hence, median weight is 56.67 kg.

Question:

The lengths of 40 leaves of a plant are measured correctly to the nearest millimetre, and the data obtained is represented in the following table:

Find the median length of the leaves.

Solution:

Here, the classes are not in inclusive form. So, we first convert them in inclusive form by subtracting h/2 from the lower limit and adding h/2 to the upper limit of each class, where h is the difference between the lower limit of a class and the upper limit of preceding class.
Now, we have

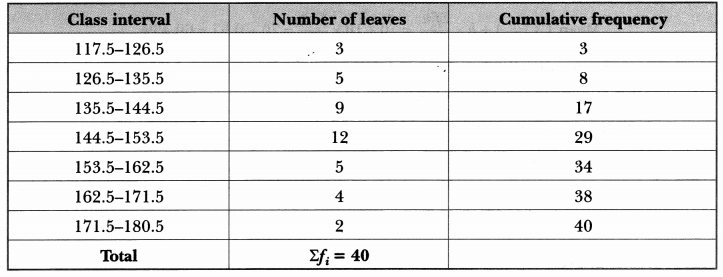
We have, n = 40
⇒ n/2 = 20 .
And, the cumulative frequency just greater than n/2 is 29 and corresponding class is 144.5 – 153.5.
So median class is 144.5 – 153.5.

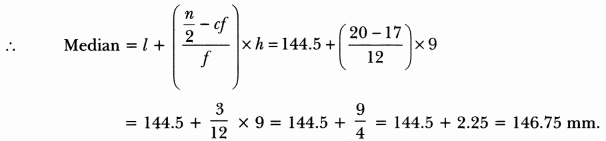
Hence, the median length of the leaves is 146.75 mm.

Question:

The distribution below gives the marks of 100 students of a class.

Draw a less than type and a more than type ogive from the given data. Hence, obtain the median marks from the graph.

Solution:

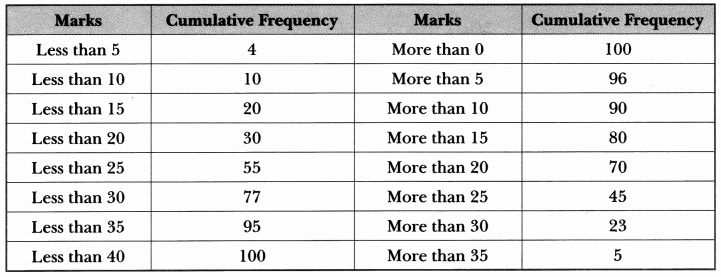
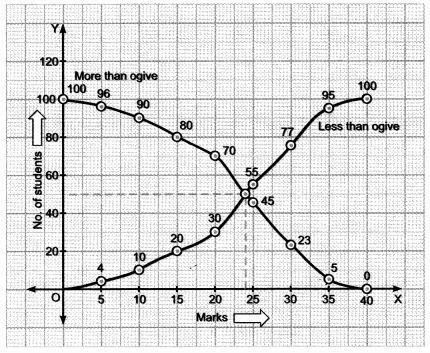
Hence, median marks = 24

Question:

During the medical check-up of 35 students of a class, their weights were recorded as follows:

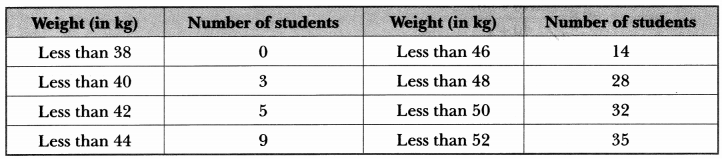
Draw a less than type ogive for the given data. Hence, obtain the median weight from the graph and verify the result by using the formula.

Solution:

To represent the data in the table graphically, we mark the upper limits of the class interval on x-axis and their corresponding cumulative frequency on y-axis choosing a convenient scale. Now, let us plot the points corresponding to the ordered pair given by (38,0), (40,3), (42,5), (44, 9), (46, 14), (48, 28), (50, 32) and (52, 35) on a graph paper and join them by a freehand smooth curve.
Thus, the curve obtained is the less than type ogive.

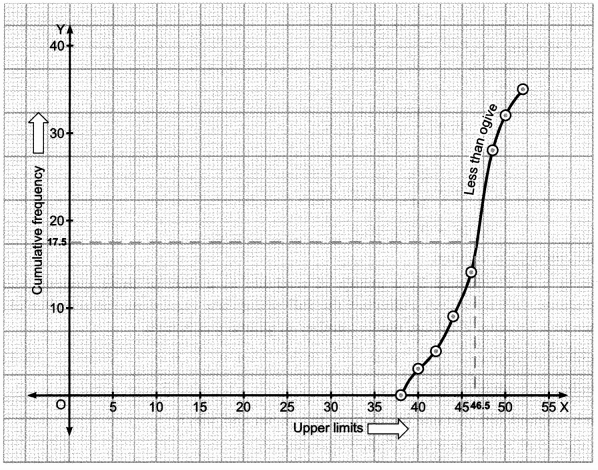
Now, locate n/2 = 35/2 = 17.5 on the y-axis,
We draw a line from this point parallel to x-axis cutting the curve at a point. From this point, draw a perpendicular line to the x-axis. The point of intersection of this perpendicular with the x-axis gives the median of the data. Here it is 46.5.
Let us make the following table in order to find median by using formula.

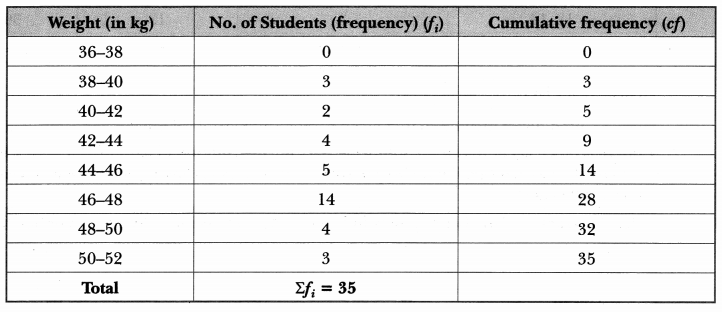
Here, n = 35, n/2 = 35/2 = 17.5, cumulative frequency greater than n/2 = 17.5 is 28 and corresponding class is 46 – 48. So median class is 46 – 48.
Now, we have l = 46, n/2 = 17.5, cf = 14, f = 14, h = 2

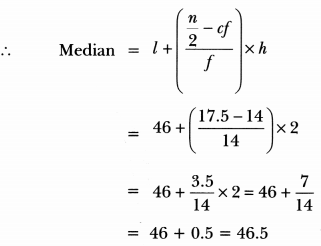
Hence, median is verified.

Question:

A survey was conducted by a group of students as a part of their environment awareness programme, in which they collected the following data regarding the number of plants in 20 housesin a locality. Find the mean number of plants per house.

Which method did you use for finding the mean and why?

Solution:

Calculation of mean number of plants per house.

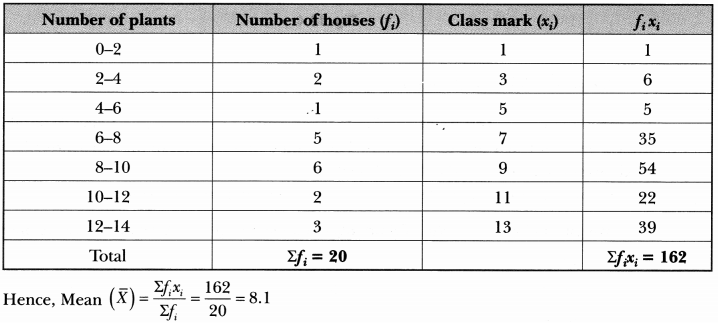
Here, we used direct method to find mean because numerical values of x; and fi are small.

Question:

A life insurance agent found the following data for distribution of ages of 100 policy holders. Calculate the median age, if policies are given only to persons having age 18 years onwards but less than 60 years.

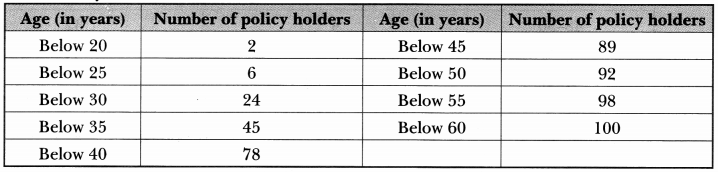
Solution:

We are given the cumulative frequency distribution. So, we first construct a frequency table from the given cumulative frequency distribution and then we will make necessary computations to compute median.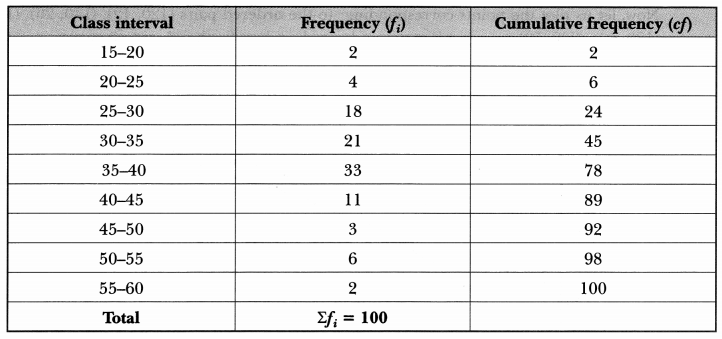

Here, n = 100
⇒ n/2 = 50

And, cumulative frequency just greater than n/2 50 is 78 and the corresponding class is 35 – 40.
So 35 – 40 is the median class.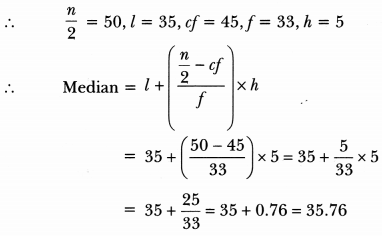

Hence, the median age is 35.76 years.

Question:

The following distribution gives the daily income of 50 workers of a factory.

Convert the distribution above to a less than type cumulative frequency distribution, and draw its ogive.

Solution:

Converting given distribution to a less than type cumulative frequency distribution, we have,

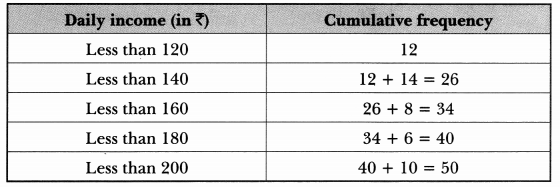
Now, let us plot the points corresponding to the ordered pairs (120, 12), (140, 26), (160, 34), (180, 40), (200, 50) on a graph paper and join them by a freehand smooth curve.

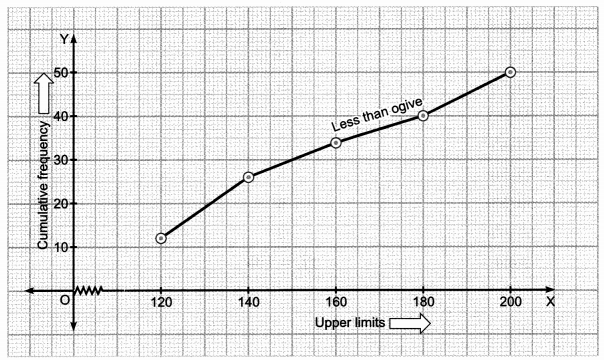
Thus, obtained curve is called the less than type ogive.

Question:

Find the mean of the following frequency distribution:

Solution:

Calculation of mean

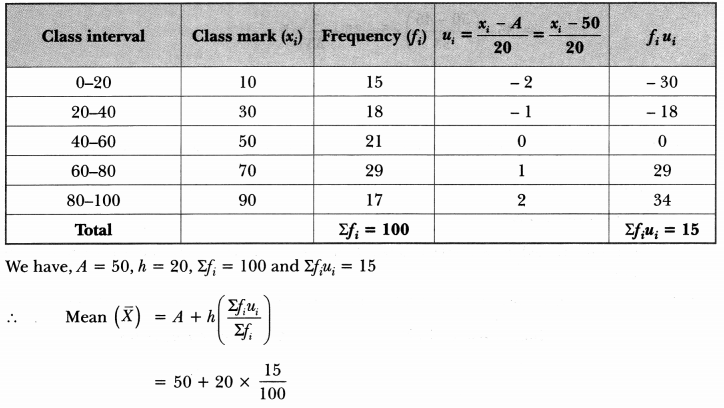
Extra Questions for Class 10 Maths Chapter 14 Long Answer Type

Question:

The mean of the following frequency table is 50. But the frequencies f₁ and f₂ in class 20 – 40 and 60 – 80 respectively are missing. Find the missing frequencies.

Solution:

Let the assumed mean A = 50 and h = 20.
Calculation of mean

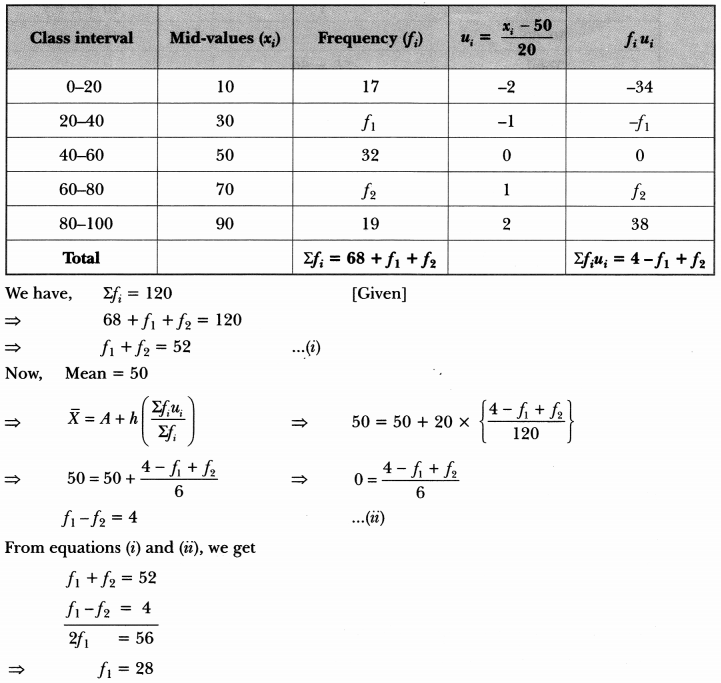
Putting the value of f₁ in equation (i), we get
28 + f₂ = 52
⇒ f₂ = 24
Hence, the missing frequencies f₁ is 28 and f₂ is 24.

Question:

If the median of the distribution given below is 28.5, find the values of x and y.

Solution:

Here, median = 28.5 and n = 60
Now, we have

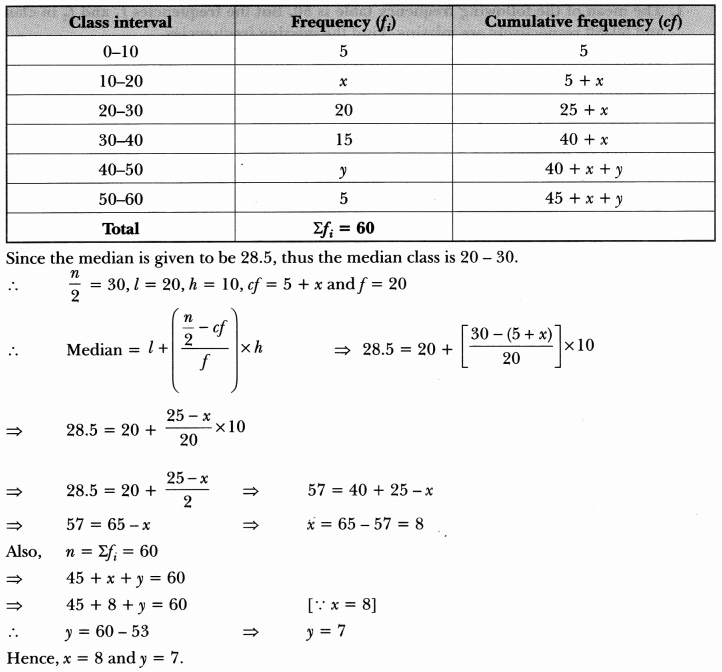
Question:

The mean of the following frequency distribution is 62.8. Find the missing frequency x.

Solution:

We have

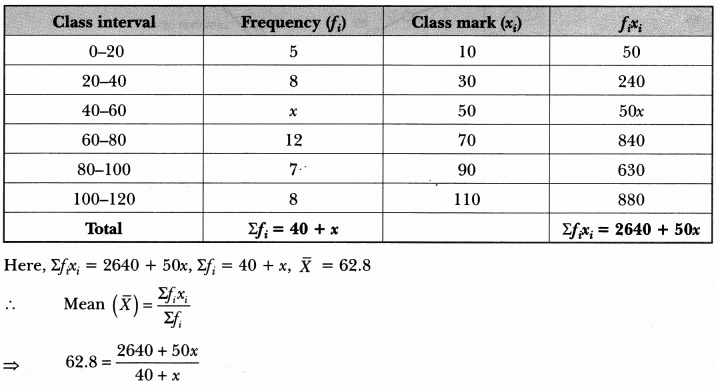
⇒ 2512 + 62.8x = 2640 + 50x
⇒ 62.8x – 50x = 2640 – 2512
⇒ 12.8x = 128
∴ x = 128/12.8 = 10
Hence, the missing frequency is 10.