We have provided you with Extra and Important Questions from Class 10 Maths Chapter 3 Pair of Linear equations in Two Variables. This Extra and Important Questions will help you to score 100% in your Board Exams. These extra questions will be helpful to revise the important topics and concepts.

Pair of Linear equations in Two Variables Class 10 Important Questions with Answers Maths Chapter 3

Extra Questions for Class 10 Maths Chapter 3 Very Short Answer Type

Question: If the lines given by 3x + 2ky = 2 and 2x + 5y + 1 = 0 are parallel, then find value of k.

Solution:
Since the given lines are parallel

Question:
Find the value of c for which the pair of equations cx – y = 2 and 6x – 2y = 3 will have infinitely many solutions.

Solution:
The given system of equations will have infinitely many solutions if c/6=−1/−2=2/3 which is not possible
∴ For no value of c, the given system of equations have infinitely many solutions.

Question: Do the equations 4x + 3y – 1 = 5 and 12x + 9y = 15 represent a pair of coincident lines?

Solution:

Given equations do not represent a pair of coincident lines.

Question:
Find the co-ordinate where the line x – y = 8 will intersect y-axis.

Solution:
The given line will intersect y-axis when x = 0.
∴0 – y = 8 ⇒ y = -8
Required coordinate is (0, -8).

Question:
Write the number of solutions of the following pair of linear equations:
x + 2y – 8 = 0, 2x + 4y = 16

Solution:


∴The given pair of linear equations has infinitely many solutions.

Question: Is the following pair of linear equations consistent? Justify your answer.
2ax + by = a, 4ax + 2by – 2a = 0; a, b≠ 0

Solution:
Yes,

∴ The given system of equations is consistent.

Question:
For all real values of c, the pair of equations
x – 2y = 8, 5x + 10y = c
have a unique solution. Justify whether it is true or false.

Solution:

So, for all real values of c, the given pair of equations have a unique solution.
∴ The given statement is true.

Question:
Does the following pair of equations represent a pair of coincident lines? Justify your answer.
x2 + y + 25 = 0, 4x+ 8y + 516 = 0.

Solution: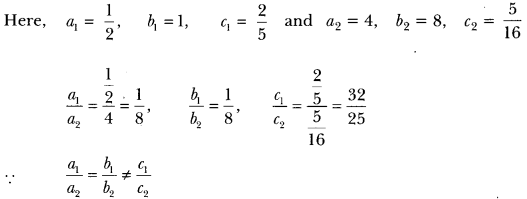

∴ The given system does not represent a pair of coincident lines.

Extra Questions for Class 10 Maths Chapter 3 Short Answer Type

Question: If x = a, y = b is the solution of the pair of equation x – y = 2 and x + y = 4, then find the value of a and b.

Solution:
x – y = 2 … (i)
x + y = 4 … (ii)
On adding (i) and (ii), we get 2x = 6 or x = 3
From (i), 3 – y ⇒ 2 = y = 1
a = 3, b = 1.

Question: On comparing the ratios a1/a2 , b1/b2, and c1/c2, find out whether the lines representing the following pair of linear equations intersect at a point, are parallel or coincident:
32 x + 53 y = 7
9x – 10y = 14

Solution: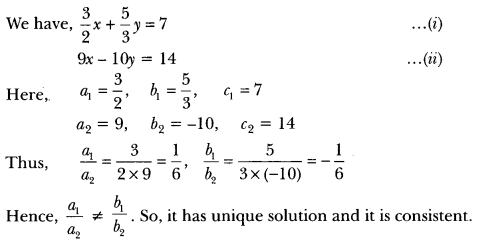

Question: On comparing the ratios a1/a2, b1/b2, and c1/c2, find out whether the lines representing the following pair of linear equations intersect at a point, are parallel or coincident:
43 x + 2y = 8;
2x + 3y = 12

Solution: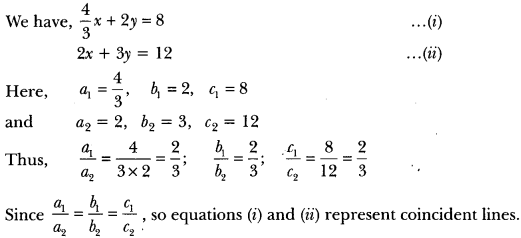

Hence, the pair of linear equations is consistent with infinitely many solutions.

Question: On comparing the ratios a1/a2, b1/b2, and c1/c2, find out whether the lines representing the following pair of linear equations intersect at a point, are parallel or coincident:
5x – 4y + 8 = 0
7x + 6y – 9 = 0
Solution: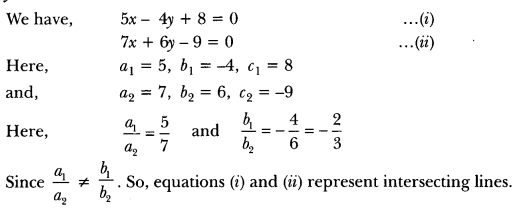

Question: On comparing the ratios a1/a2, b1/b2, and c1/c2, find out whether the lines representing the following pair of linear equations intersect at a point, are parallel or coincident:
9x + 3y + 12 = 0
18x + 6y + 24 = 0
Solution:
We have,
9x + 3y + 12 = 0
18x + 6y + 24 = 0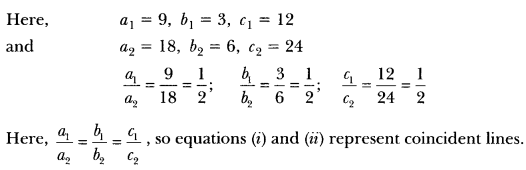

Question: On comparing the ratios a1/a2, b1/b2, and c1/c2, find out whether the lines representing the following pair of linear equations intersect at a point, are parallel or coincident:
6x – 3y + 10 = 0 .
2x – y + 9 = 0
Solution:

Question:
Solve the following linear equations:
152x – 378y = -74 and -378x + 152y = -604
Solution:
We have, 152x – 378y = -74 …(i)
-378x + 152y = -604 ……(ii)

Putting the value of x in (iii), we get
2 + y = 3 ⇒ y = 1
Hence, the solution of given system of equations is x = 2, y = 1.

Question:
Solve for x and y

Solution: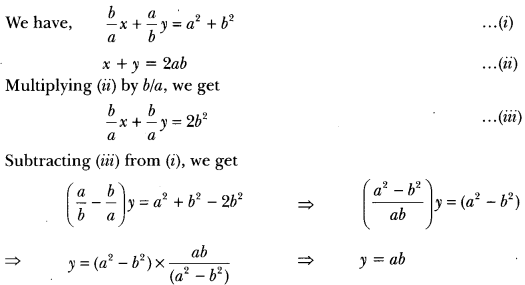

Putting the value of y in (ii), we get
x + ab = 2ab ⇒ x = 2ab – ab ⇒ x = ab
∴ x = ab, y = ab

Question:
(i) For which values of a and b does the following pair of linear equations have an infinite number of solutions?
2x + 3y = 7
(a – b)x + (a + b)y = 3a + b – 2
(ii) for which value of k will the following pair of linear equations have no solution?
3x + y = 1
(2k – 1)x + (k – 1)y = 2k + 1

Solution:
(i) We have, 2x + 3y = 7
(a – b) x + (a + b) y = 3a + b – 2 … (ii)
Here, a1 = 2, b1 = 3, c1 = 7 and
a2 = a – b, b2 = a + b, c2 = 3a + b – 2
For infinite number of solutions, we have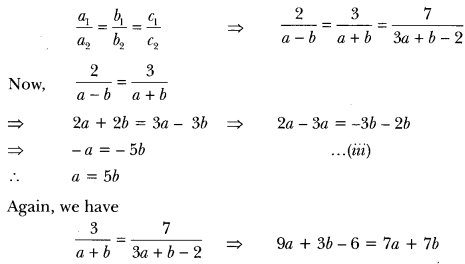

⇒ 9a – 7a + 3b – 75 -6 = 0 ⇒ 2a – 45 – 6 = 0 => 2a – 4b = 6
⇒ a – 2b = 3 …(iv)
Putting a = 5b in equation (iv), we get
56 – 2b = 3 or 3b = 3 i.e., b = 33 =1
Putting the value of b in equation (ii), we get a = 5(1) = 5
Hence, the given system of equations will have an infinite number of solutions for a = 5 and b = 1.

(ii) We have, 3x + y = 1, 3x + y − 1 = 0 …(i)
(2k – 1) x + (k – 1) y = 2k + 1
⇒ (2k – 1) x + (k – 1) y – (2k + 1) = 0 ……(ii)
Here, a1 = 3, b1 = 1, C1 = -1
a2 = 2k – 1, b2 = k – 1, C2 = -(2k + 1)
For no solution, we must have

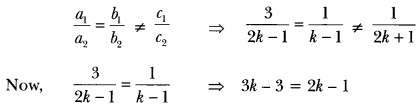
⇒ 3k – 2k = 3 – 1 ⇒ k = 2
Hence, the given system of equations will have no solutions for k = 2.

Question: Five years ago, A was thrice as old as B and ten years later, A shall be twice as old as B. What are the present ages of A and B?

Solution:
Let the present ages of B and A be x years and y years respectively. Then
B’s age 5 years ago = (x – 5) years
and A’s age 5 years ago = (- 5) years
(-5) = 3 (x – 5) = 3x – y = 10 …….(i)
B’s age 10 years hence = (x + 10) years
A’s age 10 years hence = (y + 10) years
y + 10 = 2 (x + 10) = 2x – y = -10 …….. (ii)
On subtracting (ii) from (i) we get x = 20
Putting x = 20 in (i) we get
(3 × 20) – y = 10 ⇒ y = 50
∴ x = 20 and y = 50
Hence, B’s present age = 20 years and A’s present age = 50 years.

Question:
A fraction becomes when 13 is subtracted from the numerator and it becomes 14 when 8 is added to its denominator. Find the fraction.

Solution:
Let the numerator be x and denominator be y.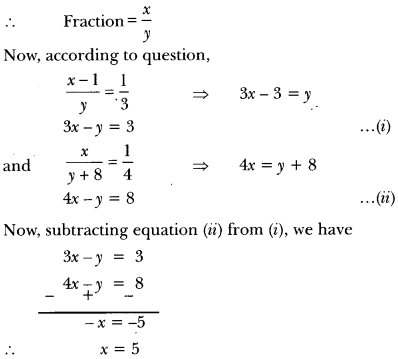

Putting the value of x in equation (i), we have
3 × 5 – y = 3 ⇒ 5 – y = 3 ⇒ 15 – 3 = y
∴ y = 12
Hence, the required fraction is 512

Question:
Solve the following pairs of equations by reducing them to a pair of linear equations:

Solution:

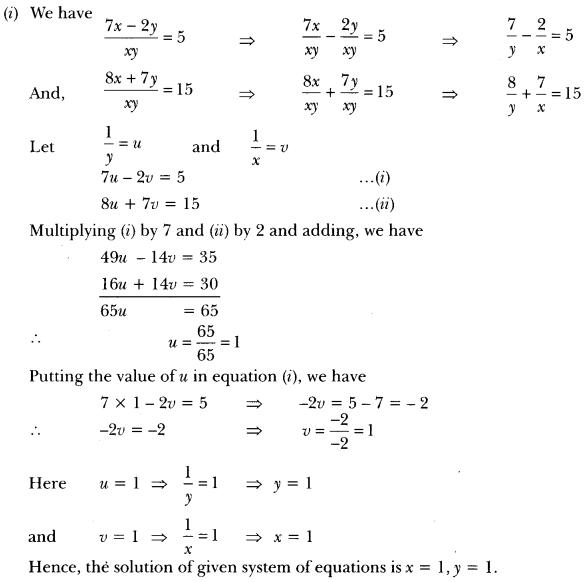
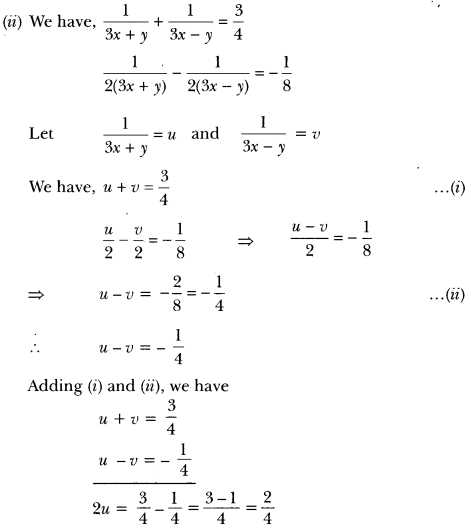
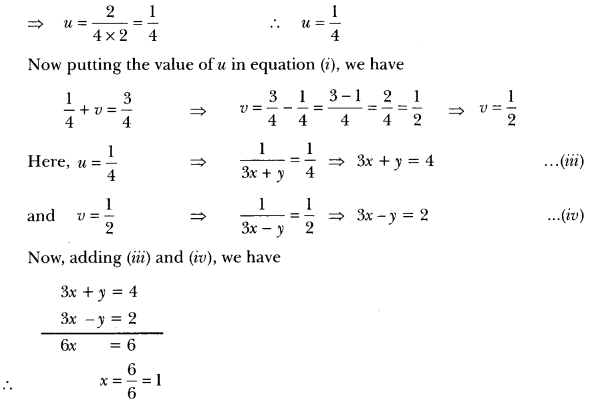
Putting the value of x in equation (iii), we have
3 x 1 + y = 4
⇒ y = 4 – 3 = 1
Hence, the solution of given system of equations is x = 1, y = 1

Question: Solve the following pair of equations for x and y.

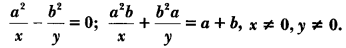
Solution:

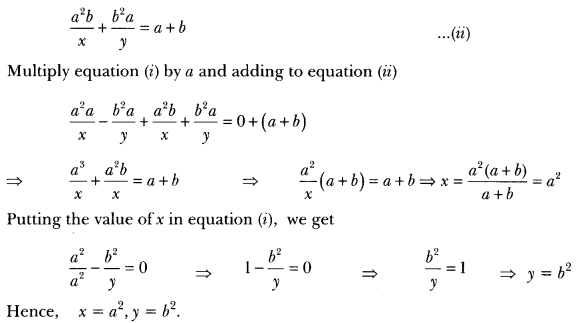
In ∆ABC, LA = x, ∠B = 3x, and ∠C = y if 3y – 5x = 30°, show that triangle is right angled.
Solution:
∠A + 2B + ∠C = 180°
(Sum of interior angles of A ABC) x + 3x + y = 180°
4x + y = 180° …(i)
3y – 5x = 30° (Given) …(ii) Multiply equation (i) by 3 and subtracting from eq. (ii), we get
-17x = – 510 = x = 910 = 30°
17 then _A = x = 30° and 2B = 3x = 3 X 30o = 90°
∠C = y = 180° – (∠A + ∠B) = 180° – 120° = 60°
∠A = 30°, ∠B = 90°, ∠C = 60° Hence ∆ABC is right triangle right angled at B.

Question:
In Fig. 3.1, ABCDE is a pentagon with BE|CD and BC||DE. BC is perpendicular to CD. If the perimeter of ABCDE is 21 cm. Find the value of x and y.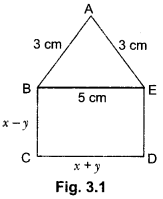

Solution:
Since BC||DE and BE||CD with BC||CD.
BCDE is a rectangle.
Opposite sides are equal BE = CD
∴ x + y = 5 …… (i)
DE = BC = x – y
Since perimeter of ABCDE is 21 cm.
AB + BC + CD + DE + EA = 21
3 + x – y + x + y + x – y + 3 = 21 ⇒ 6 + 3x – y = 21
3x – y = 15 ….. (iii)
Adding (i) and (ii), we get
4x = 20 ⇒ x = 5
On putting the value of x in (i), we get y = 0
Hence, x = 5 and y = 0.

Extra Questions for Class 10 Maths Chapter 3 Long Answer Type

Question: Form the pair of linear equations in this problem, and find its solution graphically: 10 students of Class X took part in a Mathematics quiz. If the number of girls is 4 more than the number of boys, find the number of boys and girls who took part in the quiz.

Solution:
Let x be the number of girls and y be the number of boys.
According to question, we have
x = y + 4
⇒ x – y = 4 ……(i)
Again, total number of students = 10
Therefore, x + y = 10 …(ii)
Hence, we have following system of equations
x – y = 4
and x + y = 10
From equation (i), we have the following table: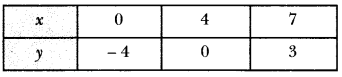

From equation (ii), we have the following table:

Plotting this, we have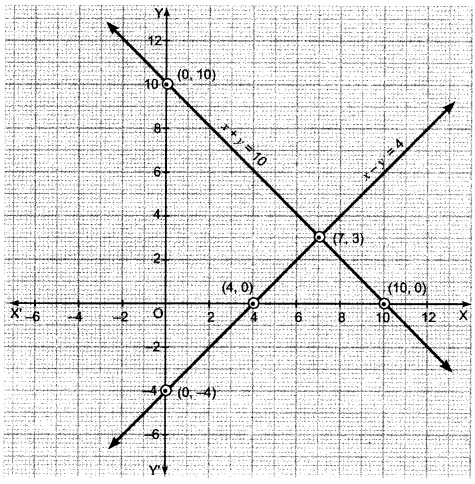

Here, the two lines intersect at point (7,3) i.e., x = 7, y = 3.
So, the number of girls = 7
and number of boys = 3.

Question:
Show graphically the given system of equations
2x + 4y = 10 and 3x + 6y = 12 has no solution.

Solution:
We have, 2x + 4y = 10
⇒ 4y = 10 – 2x ⇒ y = 5−x2
Thus, we have the following table:

Plot the points A (1, 2), B (3, 1) and C (5,0) on the graph paper. Join A, B and C and extend it on both sides to obtain the graph of the equation 2x + 4y = 10.
We have, 3x + 6y = 12
⇒ 6y = 12 – 3x ⇒ y = 4−x2
Thus, we have the following table :

Plot the points D (2, 1), E (0, 2) and F (4,0) on the same graph paper. Join D, E and F and extend it on both sides to obtain the graph of the equation 3x + 6y = 12.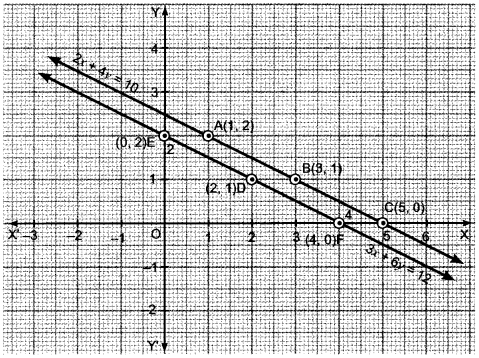

We find that the lines represented by equations 2x + 4y = 10 and 3x + y = 12 are parallel. So, the two lines have no common point. Hence, the given system.of equations has no solution.

Question: Formulate the following problems as a pair of equations, and hence find their solutions:
(i) Ritu can row downstream 20 km in 2 hours, and upstream 4 km in 2 hours. Find her speed of rowing in still water and the speed of the current.
(ii) Roobi travels 300 km to her home partly by train and partly by bus. She takes 4 hours if she travels 60 km by bus and the remaining by train. If she travels 100 km by bus and the remaining by train, she takes 10 minutes longer. Find the speed of the train and the bus separately.

Solution:
(i) Let her speed of rowing in still water be x km/h and the speed of the current be y km/h.
Case I: When Ritu rows downstream
Her speed (downstream) = (x + y) km/h

Putting the value of x in equation (i), we have
6 + y = 10 ⇒ y = 10 – 6 = 4
Hence, speed of Ritu in still water = 6 km/h.
and speed of current = 4 km/h.

(ii) Let the speed of the bus be x km/h and speed of the train be y km/h.
According to question, we have

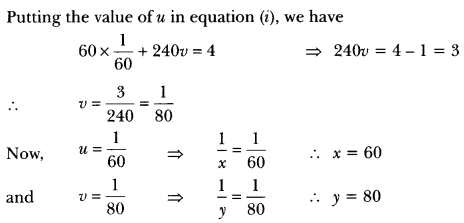
Question: The sum of a two digit number and the number formed by interchanging its digits is 110. If 10 is subtracted from the first number, the new number is 4 more than 5 times the sum of the digits in the first number. Find the first number.

Solution:
Let the digits at unit and tens places be x and y respectively.
Then, number = 10y + x …(i)
Number formed by interchanging the digits = 10x + y
According to the given condition, we have
(10y + x) + (10x + y) = 110
⇒ 11x + 11y = 110
⇒ x + y – 10 = 0
Again, according to question, we have
(10y + x) – 10 = 5 (x + y) + 4
⇒ 10y + x – 10 = 5x + 5y + 4
⇒ 10y + x – 5x – 5y = 4 + 10
5y – 4x = 14 or 4x – 5y + 14 = 0
By using cross-multiplication, we have .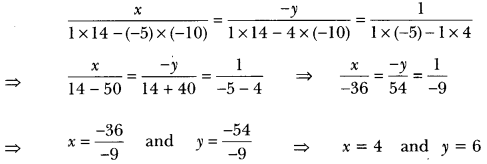

Putting the values of x and y in equation (i), we get
Number 10 × 6 + 4 = 64.

Question:
Jamila sold a table and a chair for 1050, thereby making a profit of 10% on the table and 25% on the chair. If she had taken a profit of 25% on the table and 10% on the chair she would have got 1065. Find cost price of each.

Solution:
Let cost price of table be ₹x and the cost price of the chair be ₹y.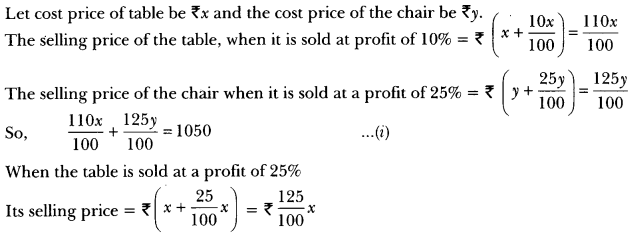
”

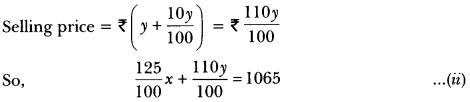
From equation (i) and (ii) we get
110x + 125y = 105000
and 125x + 110y = 106500
On adding and subtracting these equations, we get
235x + 235y = 211500
and 15x – 15y = 1500
i.e., x + y = 900 …(iii)
x – y = 100 …… (iv)
Solving equation (iii) and (iv) we get
x = 500, y = 400
So, the cost price of the table is ₹500 and the cost price of the chair is ₹400.

Question: Solve the following pairs of linear equations by the elimination method and the substitution method:
(i) 3x – 5y – 4 = 0 and 9x = 2y + 7
(ii) x2+2y3 = -1 and x – y3 = 3

Solution:
(i) We have, 3x – 5y – 4 = 0
⇒ 3x – 5y = 4 …….(i)
Again, 9x = 2y + 7
9x – 2y = 7 …(ii)

By Elimination Method:
Multiplying equation (i) by 3, we get
9x – 15y = 12 … (iii)
Subtracting (ii) from (iii), we get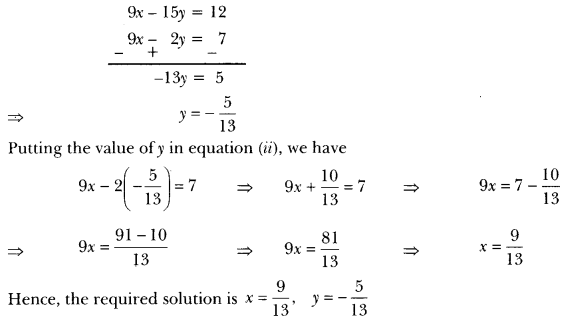

By Substitution Method:
Expressing x in terms of y from equation (i), we have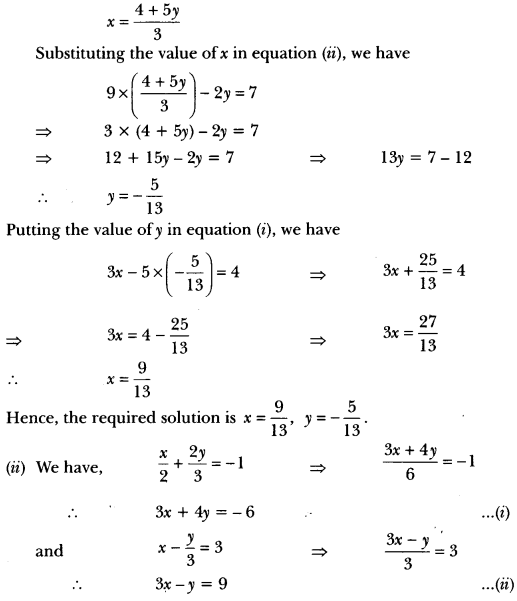

By Elimination Method:
Subtracting (ii) from (i), we have
5y = – 15 or y = – 55 = -3
Putting the value of y in equation (i), we have
3x + 4 × (-3) = -6 ⇒ 3x = – 6 + 12
∴ 3x – 12 = -6 ⇒ 3x = 6
∴ x = 63 = 2
Hence, solution is x = 2, y = -3.

By Substitution Method:
Expressing x in terms of y from equation (i), we have
3 × (−6−4y3) – y = 9 ⇒ -6 – 4y – y = 9 ⇒ -6 – 5y = 9
Substituting the value of x in equation (ii), we have
∴ -5y = 9 + 6 = 15
y = – 155 = – 3
Putting the value of y in equation (i), we have
3x + 4 × (-3) = -6 ⇒ 3x – 12 = -6
∴ 3x = 12 – 6 = 6
∴ x = 63 = 2
Hence, the required solution is x = 2, y = – 3.

Question: 8 men and 12 boys can finish a piece of work in 10 days while 6 men and 8 boys can finish it in 14 days. Find the time taken by one man alone and that by one boy alone to finish the work.

Solution:
Let one man alone can finish the work in x days and one boy alone can finish the work in y days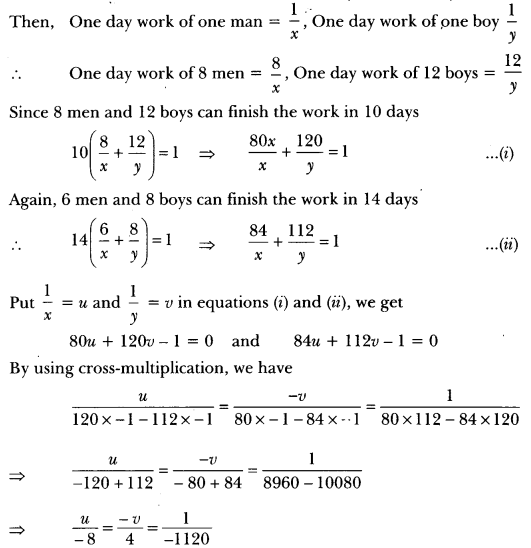


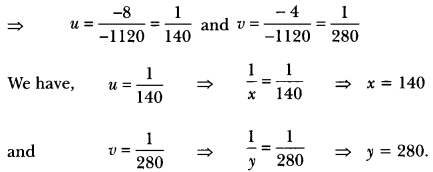
Hence, one man alone can finish the work in 140 days and one boy alone can finish the work in 280 days.

Question:
A boat covers 25 km upstream and 44 km downstream in 9 hours. Also, it covers 15 km upstream and 22 km downstream in 5 hours. Find the speed of the boat in still water and that of the stream.

Solution:
Let the speed of the boat in still water be x km/h and that of the stream be y km/h. Then,
Speed upstream (x – y) km/h
Speed downstream (x + y) km/h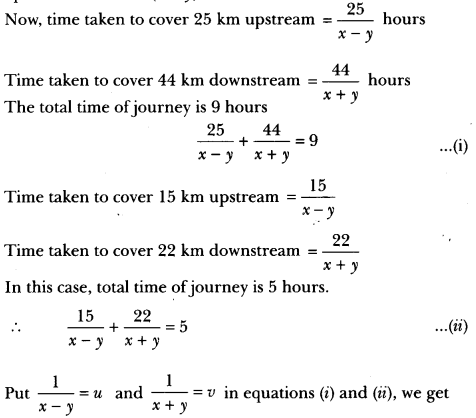

25u + 44v = 9 ⇒ 25u + 44v – 9 = 0 …(iii)
15u + 22v = 5 ⇒ 15u + 22v – 5 = 0 …(iv)
By cross-multiplication, we have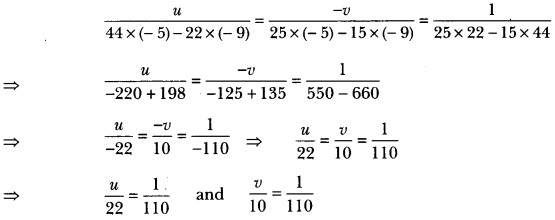


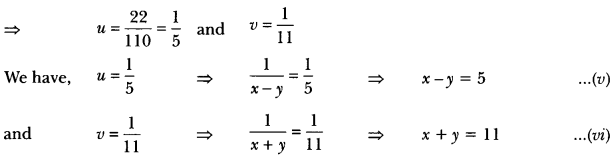
Solving equations (v) and (vi), we get x = 8 and y = 3.
Hence, speed of the boat in still water is 8 km/h and speed of the stream is 3 km/h.